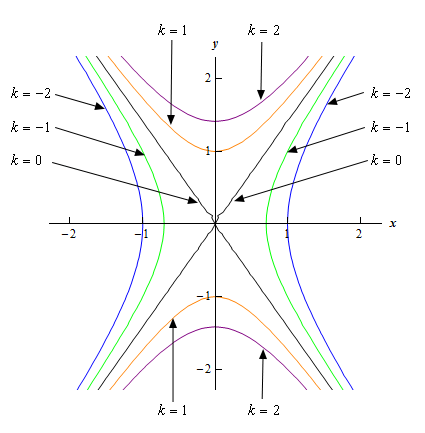Calculus III - Functions of Several Variables

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 12.5 : Functions of Several Variables

Back to Problem List

7. Identify and sketch the level curves (or contours) for the following function.

${y^2} = 2{x^2} + z$

Show All Steps Hide All Steps

Start Solution

We know that level curves or contours are given by setting $z = k$ . Doing this in our equation gives,

${y^2} = 2{x^2} + k$ Show Step 2

For this problem the value of $k$ will affect the type of graph of the level curve.

First, if $k = 0$ the equation will be,

${y^2} = 2{x^2}\hspace{0.5in} \Rightarrow \hspace{0.5in}y = \pm \sqrt 2 \,\,x$

So, in this case the level curve (actually curves if you think about it) will be two lines through the origin. One is increasing and the other is decreasing.

Next, let’s take a look at what we get if $k > 0$ . In this case a quick rewrite of the equation from Step 2 gives,

$\frac{{{y^2}}}{k} - \frac{{2{x^2}}}{k} = 1$

Because we know that $k$ is positive we see that we have a hyperbola with the $y$ term the positive term and the $x$ term the negative term. This means that the hyperbola will be symmetric about the $y$ -axis and opens up and down.

Finally, what do we get if $k < 0$ . In this case the equation is,

$- \frac{{2{x^2}}}{k} + \frac{{{y^2}}}{k} = 1$

Now, be careful with this equation. In this case we have negative values of $k$ . This means that the $x$ term is in fact positive (the minus sign will cancel against the minus sign in the $k$ ). Likewise, the $y$ term will be negative (it’s got a negative $k$ in the denominator). Therefore, we’ll have a hyperbola that is symmetric about the $x$ -axis and opens right and left.

Show Step 3

Below is a sketch of some level curves for some values of $k$ for this function.