Section 17.5 : Stokes' Theorem
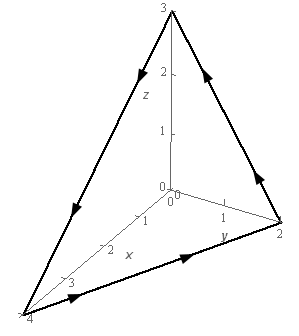
4. Use Stokes’ Theorem to evaluate \(\displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F = \left( {3y{x^2} + {z^3}} \right)\,\vec i + {y^2}\,\vec j + 4y{x^2}\,\vec k\) and \(C\) is is triangle with vertices \(\left( {0,0,3} \right)\), \(\left( {0,2,0} \right)\) and \(\left( {4,0,0} \right)\). \(C\) has a counter clockwise rotation if you are above the triangle and looking down towards the \(xy\)-plane. See the figure below for a sketch of the curve.
Show All Steps Hide All Steps
Start SolutionOkay, we are going to use Stokes’ Theorem in the following direction.
\[\int\limits_{C}{{\vec F\centerdot d\vec r}} = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\]So, let’s first compute \({\mathop{\rm curl}\nolimits} \vec F\)since that is easy enough to compute and might be useful to have when we go to determine the surface \(S\) we’re going to integrate over.
The curl of the vector field is then,
\[{\mathop{\rm curl}\nolimits} \vec F = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\{\displaystyle \frac{\partial }{{\partial x}}}&{\displaystyle \frac{\partial }{{\partial y}}}&{\displaystyle \frac{\partial }{{\partial z}}}\\{3y{x^2} + {z^3}}&{{y^2}}&{4y{x^2}}\end{array}} \right| = 4{x^2}\vec i + 3{z^2}\vec j - 3{x^2}\vec k - 8yx\vec j = \underline {4{x^2}\vec i + \left( {3{z^2} - 8yx} \right)\vec j - 3{x^2}\vec k} \] Show Step 2Now we need to find a surface \(S\) with an orientation that will have a boundary curve that is the curve shown in the problem statement, including the correct orientation.
In this case we can see that the triangle looks like the portion of a plane and so it makes sense that we use the equation of the plane containing the three vertices for the surface here.
The curl of the vector field looks a little messy so using a plane here might be the best bet from this perspective as well. It will (hopefully) not make the curl of the vector field any messier and the normal vector, which we’ll get from the equation of the plane, will be simple and so shouldn’t make the curl of the vector field any worse.
Show Step 3Determining the equation of the plane is pretty simple. We have three points on the plane, the vertices, and so we can quickly determine the equation.
First, let’s “label” the points as follows,
\[P = \left( {4,0,0} \right)\hspace{0.25in}\hspace{0.25in}Q = \left( {0,2,0} \right)\hspace{0.25in}\hspace{0.25in}R = \left( {0,0,3} \right)\]Then two vectors that must lie in the plane are,
\[\overrightarrow {QP} = \left\langle {4, - 2,0} \right\rangle \hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\overrightarrow {QR} = \left\langle {0, - 2,3} \right\rangle \]To write the equation of a plane recall that we need a normal vector to the plane. Now, we know that the cross product of these two vectors will be orthogonal to both of the vectors. Also, since both of the vectors lie in the plane the cross product will also be orthogonal, or normal, to the plane. In other words, we can use the cross product of these two vectors as the normal vector to the plane.
The cross product is,
\[\overrightarrow {QP} \times \overrightarrow {QR} = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\4&{ - 2}&0\\0&{ - 2}&3\end{array}} \right| = - 6\vec i - 12\vec j - 8\vec k\]Now we can use any of the points in our equation. We’ll use \(Q\) for our point. The equation of the plane is then,
\[\begin{array}{r} - 6\left( {x - 0} \right) - 12\left( {y - 2} \right) - 8\left( {z - 0} \right) = 0\hspace{0.25in} \to \hspace{0.25in}\, - 6x - 12y - 8z = - 24\\ \underline {3x + 6y + 4z = 12} \,\,\,\,\end{array}\]Note that we divided the equation by –2 to make the equation a little “nicer” to work with.
Show Step 4We now need to determine the orientation of the normal vectors that will induce a positive orientation of the boundary curve, \(C\), that matches the orientation that was given in the problem statement.
Remember that what we want to do here is think of ourselves as walking along the boundary curve of the surface in the direction indicated while our left hand is over the plane. We now need to determine if we are walking along the top or bottom of the plane.
If we are walking along the top of the plane then our heads, and hence the normal vectors, will be pointing in a generally upwards direction. On the other hand, if we are walking along the bottom of the plane then our heads, and hence the normal vectors, will be pointing generally downwards.
To help visualize this for our plane it might help to cut out a triangular piece of paper that we can use to represent the plane. The edge of the piece of paper will then represent the boundary curve. Next cut out a stick figure and put a face on one side so we know which direction we’ll be walking and brightly color the left hand to make it really clear which side is the left side.
Now, hold the piece of paper so that it looks vaguely like the surface we’re working with and put the stick figure on the edge with the face pointing in the direction the curve is moving and the left hand over the cup/bowl. Doing this we’ll quickly see that we must be walking along the top of the surface. Therefore, the normal vectors on the surface need to be pointing in a generally upwards direction (and hence will have a positive \(z\) component).
Show Step 5We now need to start thinking about actually computing the integral. We’ll write the equation of the surface as,
\[z = 3 - \frac{3}{4}x - \frac{3}{2}y\]Recall that if we aren’t going to parameterize the surface we need it to be written as \(z = g\left( {x,y} \right)\) so that the magnitude of the normal vector will eventually cancel.
Now, that we have the surface written in the “proper” form let’s define,
\[f\left( {x,y,z} \right) = z - 3 + \frac{3}{4}x + \frac{3}{2}y = 0\]The unit normal vector for the surface is then,
\[\vec n = \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}} = \frac{{\left\langle {\frac{3}{4},\frac{3}{2},1} \right\rangle }}{{\left\| {\nabla f} \right\|}}\]We didn’t compute the magnitude of the gradient since we know that it will just cancel out when we start working with the integral.
Note as well that this does have the correct orientation because the \(z\) component is positive.
Next, we’ll need to compute the following dot product.
\[\begin{align*}{\mathop{\rm curl}\nolimits} \vec F\centerdot \vec n & = \left\langle {4{x^2},\left( {3{{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^2} - 8yx} \right), - 3{x^2}} \right\rangle \centerdot \frac{{\left\langle {\frac{3}{4},\frac{3}{2},1} \right\rangle }}{{\left\| {\nabla f} \right\|}}\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left( {3{x^2} + \frac{9}{2}{{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^2} - 12xy - 3{x^2}} \right)\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left[ {\frac{9}{2}{{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^2} - 12xy} \right]\end{align*}\]Don't forget to plug the equation of the surface into the curl of the vector field.
Show Step 6Now, applying Stokes’ Theorem to the integral and converting to a “normal” double integral gives,
\[\begin{align*}\int\limits_{C}{{\vec F\centerdot d\vec r}} & = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\\ & = \iint\limits_{S}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left[ {\frac{9}{2}{{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^2} - 12xy} \right]dS}}\\ & = \iint\limits_{D}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left[ {\frac{9}{2}{{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^2} - 12xy} \right]\left\| {\nabla f} \right\|dA}}\\ & = \iint\limits_{D}{{\frac{9}{2}{{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^2} - 12xy\,dA}}\end{align*}\] Show Step 7To finish this integral we just need to determine \(D\). In this case \(D\) just the triangle in the \(xy\)-plane that lies below the plane. Here is a quick sketch of \(D\).
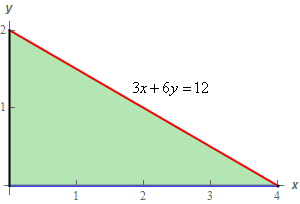
The integral doesn’t seem to suggest one integration order over the other so let’s use the following set of limits for our integral.
\[\begin{array}{c}0 \le x \le 4\\ 0 \le y \le 2 - \frac{1}{2}x\end{array}\]The integral is then,
\[\begin{align*}\int\limits_{C}{{\vec F\centerdot d\vec r}} & = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\\ & = \int_{0}^{4}{{\int_{0}^{{2 - \frac{1}{2}x}}{{\frac{9}{2}{{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^2} - 12xy\,dy}}\,dx}}\\ & = \int_{0}^{4}{{\left. {\left( { - {{\left( {3 - \frac{3}{4}x - \frac{3}{2}y} \right)}^3} - 6x{y^2}} \right)} \right|_0^{2 - \frac{1}{2}x}\,dx}}\\ & = \int_{0}^{4}{{{{\left( {3 - \frac{3}{4}x} \right)}^3} - 6x{{\left( {2 - \frac{1}{2}x} \right)}^2}\,dx}}\\ & = \int_{0}^{4}{{{{\left( {3 - \frac{3}{4}x} \right)}^3} - 24x + 12{x^2} - \frac{3}{2}{x^3}\,dx}}\\ & = \left. {\left( { - \frac{1}{3}{{\left( {3 - \frac{3}{4}x} \right)}^4} - 12{x^2} + 4{x^3} - \frac{3}{8}{x^4}} \right)} \right|_0^4\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 5}}\end{align*}\]