Section 17.4 : Surface Integrals of Vector Fields
1. Evaluate \( \displaystyle \iint\limits_{S}{{\vec F\centerdot \,d\vec S}}\) where \(\vec F = 3x\,\vec i + 2z\,\vec j + \left( {1 - {y^2}} \right)\vec k\) and \(S\) is the portion of \(z = 2 - 3y + {x^2}\) that lies over the triangle in the
\)-plane with vertices \(\left( {0,0} \right)\), \(\left( {2,0} \right)\) and \(\left( {2, - 4} \right)\) oriented in the negative z-axis direction.Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
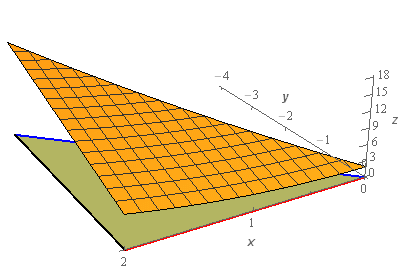
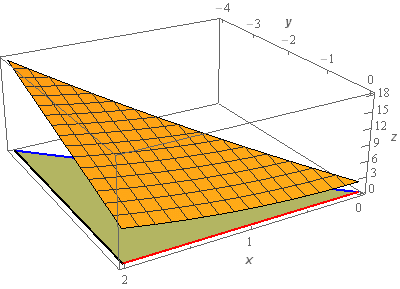
We included a sketch with traditional axes and a sketch with a set of “box” axes to help visualize the surface.
The orange surface is the sketch of \(z = 2 - 3y + {x^2}\) that we are working with in this problem. The greenish triangle below the surface is the triangle referenced in the problem statement that lies below the surface. This triangle will be the region \(D\) for this problem.
Here is a quick sketch of \(D\) just to get a better view of it than the mostly obscured view in the sketch above.
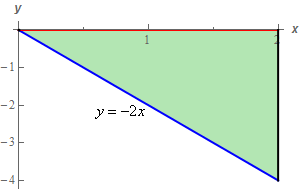
We’ll decide which set to use in the integral once we get that set up.
Show Step 2Let’s get the integral set up now. In this case the we can write the equation of the surface as follows,
\[f\left( {x,y,z} \right) = 2 - 3y + {x^2} - z = 0\]A unit normal vector for the surface is then,
\[\vec n = \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}} = \frac{{\left\langle {2x, - 3, - 1} \right\rangle }}{{\left\| {\nabla f} \right\|}}\]We didn’t compute the magnitude of the gradient since we know that it will just cancel out when we start working with the integral.
Note as well that, in this case, the normal vector we computed above has the correct orientation. We were told in the problem statement that the orientation was in the negative \(z\)-axis direction and this means that the normal vector should always have a downwards direction (i.e. a negative \(z\) component) and this one does.
Show Step 3Next, we’ll need to compute the following dot product.
\[\begin{align*}\vec F\left( {x,y,2 - 3y + {x^2}} \right)\centerdot \vec n & = \left\langle {3x,2\left( {2 - 3y + {x^2}} \right),1 - {y^2}} \right\rangle \centerdot \frac{{\left\langle {2x, - 3, - 1} \right\rangle }}{{\left\| {\nabla f} \right\|}}\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left( {6{x^2} - 6\left( {2 - 3y + {x^2}} \right) - \left( {1 - {y^2}} \right)} \right)\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left( {{y^2} + 18y - 13} \right)\end{align*}\]Remember that we needed to plug in the equation of the surface, \(z = 2 - 3y + {x^2}\), into \(z\) in the vector field!
The integral is then,
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{S}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left( {{y^2} + 18y - 13} \right)\,dS}}\\ & = \iint\limits_{D}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left( {{y^2} + 18y - 13} \right)\left\| {\nabla f} \right\|\,dA}}\\ & = \iint\limits_{D}{{{y^2} + 18y - 13\,dA}}\end{align*}\]As noted above we didn’t need to compute the magnitude of the gradient since it would just cancel out when we converted the surface integral into a “normal” double integral.
Also, recall that \(D\) was given in Step 1. We had two sets of limits to use here but it seems like the first set is probably just as easy to use so we’ll use that one in the integral.
Show Step 4Now all that we need to do is evaluate the double integral and that shouldn’t be too difficult at this point.
Here is the integral,
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{D}{{{y^2} + 18y - 13\,dA}}\\ & = \int_{0}^{2}{{\int_{{ - 2x}}^{0}{{{y^2} + 18y - 13\,dy}}\,dx}}\\ & = \int_{0}^{2}{{\left. {\left( {\frac{1}{3}{y^3} + 9{y^2} - 13y} \right)} \right|_{ - 2x}^0\,dx}}\\ & = \int_{0}^{2}{{\frac{8}{3}{x^3} - 36{x^2} - 26x\,dx}}\\ & = \left. {\left( {\frac{2}{3}{x^4} - 12{x^3} - 13{x^2}} \right)} \right|_0^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{{412}}{3}}}\end{align*}\]