I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 15.9 : Surface Area
1. Determine the surface area of the portion of \(2x + 3y + 6z = 9\) that is in the 1st octant.
Show All Steps Hide All Steps
Start SolutionOkay, let’s start off with a quick sketch of the surface so we can get a feel for what we’re dealing with.
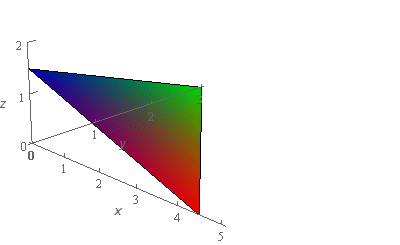
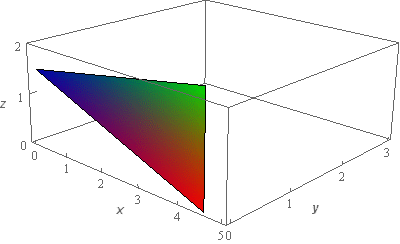
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface.
Show Step 2Let’s first set up the integral for the surface area of this surface. This surface doesn’t force a region \(D\) in any of the coordinates planes so we can work with any of them that we want to.
So, let’s work with \(D\) in the \(xy\)-plane. This, in turn, means we’ll first need to solve the equation of the plane for \(z\) to get,
\[z = \frac{3}{2} - \frac{1}{3}x - \frac{1}{2}y\]Now, the integral for the surface area is,
\[S = \iint\limits_{D}{{\sqrt {{{\left[ { - \frac{1}{3}} \right]}^2} + {{\left[ { - \frac{1}{2}} \right]}^2} + 1} \,dA}} = \iint\limits_{D}{{\sqrt {\frac{{49}}{{36}}} \,dA}} = \iint\limits_{D}{{\frac{7}{6}\,dA}}\] Show Step 3Now, we’ll need to figure out the region \(D\) we’ll need to use in our integral. In this case \(D\) is simply the triangle in the \(xy\)-plane that is directly below the plane. Here is a quick sketch of \(D\).
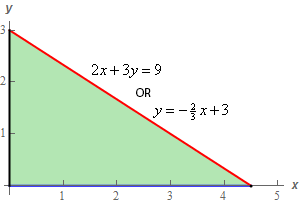
The equation of the hypotenuse can be simply found by plugging \(z = 0\) into the equation for the plane since it is simply nothing more than where the plane intersects with the \(xy\)‑plane.
Here are a set of limits for this \(D\).
\[\begin{array}{c} \displaystyle 0 \le x \le \frac{9}{2}\\ \displaystyle 0 \le y \le - \frac{2}{3}x + 3\end{array}\] Show Step 4Now, normally we’d proceed to evaluate the integral at this point and we could do that if we wanted to. However, we don’t need to do that in this case.
Let’s do a quick rewrite the surface area integral as follows.
\[S = \frac{7}{6}\iint\limits_{D}{{dA}}\]At this point we can see that the integrand of the integral is only 1.
Show Step 5Because the integrand is only 1 we can use the fact that the value of this integral is nothing more than the area of \(D\) and since \(D\) is just a right triangle we can quickly compute the area of \(D\).
The surface area is then,
\[S = \frac{7}{6}\iint\limits_{D}{{dA}} = \frac{7}{6}\left( {{\mbox{Area of }}D} \right) = \frac{7}{6}\left( {\frac{1}{2}} \right)\left( {\frac{9}{2}} \right)\left( 3 \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{63}}{8}}}\]Don’t forget this nice little fact about the value of \(\iint\limits_{D}{{dA}}\) . It doesn’t come up often but when it does and \(D\) is an easy to compute area it can greatly reduce the amount of work for the integral evaluation.