Section 17.3 : Surface Integrals
2. Evaluate \( \displaystyle \iint\limits_{S}{{40y\,dS}}\) where \(S\) is the portion of \(y = 3{x^2} + 3{z^2}\) that lies behind \(y = 6\) .
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
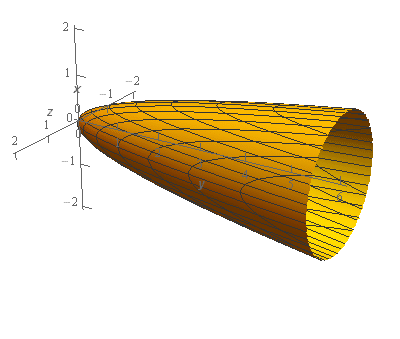
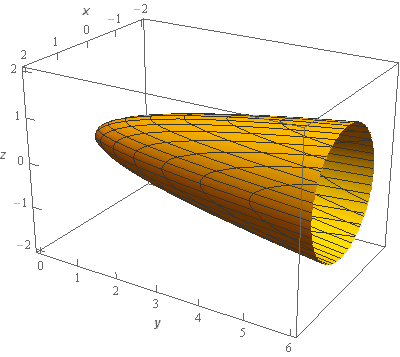
Note that the surface in this problem is only the elliptic paraboloid and does not include the “cap” at \(y = 6\). We would only include the “cap” if the problem had specified that in some manner to make it clear.
In this case \(D\) will be the circle/disk we get by setting the two equations equal or,
\[6 = 3{x^2} + 3{z^2}\hspace{0.25in} \Rightarrow \hspace{0.25in}\,{x^2} + {z^2} = 2\]So, \(D\) will be the disk \({x^2} + {z^2} \le 2\).
Show Step 2Let’s get the integral set up now. In this case the surface is in the form,
\[y = g\left( {x,z} \right) = 3{x^2} + 3{z^2}\]so we’ll use the following formula for the surface integral.
\[\iint\limits_{S}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {x,g\left( {x,z} \right),z} \right)\sqrt {{{\left( {\frac{{\partial g}}{{\partial x}}} \right)}^2} + 1 + {{\left( {\frac{{\partial g}}{{\partial z}}} \right)}^2}} \,dA}}\]The integral is then,
\[\begin{align*}\iint\limits_{S}{{40y\,dS}} & = \iint\limits_{D}{{40\left( {3{x^2} + 3{z^2}} \right)\sqrt {{{\left( {6x} \right)}^2} + 1 + {{\left( {6z} \right)}^2}} \,dA}}\\ & = \iint\limits_{D}{{120\left( {{x^2} + {z^2}} \right)\sqrt {36\left( {{x^2} + {z^2}} \right) + 1} \,dA}}\end{align*}\]Don’t forget to plug the equation of the surface into \(y\) in the integrand and recall that \(D\) is the disk we found in Step 1.
Show Step 3Now, for this problem it should be pretty clear that we’ll want to use polar coordinates to do the integral. We’ll use the following set of polar coordinates.
\[x = r\cos \theta \hspace{0.25in}\hspace{0.25in}z = r\sin \theta \hspace{0.25in}\hspace{0.25in}{x^2} + {z^2} = {r^2}\]Also, because \(D\) is the disk \({x^2} + {z^2} \le 2\) the limits for the integral will be,
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le \sqrt 2 \end{array}\]Converting the integral to polar coordinates gives,
\[\begin{align*}\iint\limits_{S}{{40y\,dS}} & = \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 2 }}{{120{r^2}\sqrt {36{r^2} + 1} \,\left( r \right)dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 2 }}{{120{r^3}\sqrt {36{r^2} + 1} \,dr}}\,d\theta }}\end{align*}\]Don’t forget to pick up the extra \(r\) when converting the \(dA\) into polar coordinates.
Show Step 4Now all that we need to do is evaluate the double integral and this one can be a little tricky unless you’ve seen this kind of integral done before.
We’ll use the following substitution to do the integral.
\[u = 36{r^2} + 1\hspace{0.25in} \to \hspace{0.25in}du = 72r\,dr\hspace{0.25in} \to \hspace{0.25in}\frac{1}{{72}}du = r\,dr\]The problem is that this doesn’t seem to work at first glance because the differential will only get rid of one of the three \(r\)’s in front of the root. However, we can also solve the substitution for \({r^2}\) to get,
\[{r^2} = \frac{1}{{36}}\left( {u - 1} \right)\]and we can now convert the remaining two \(r\)’s into \(u\)’s.
So, using the substitution the integral becomes,
\[\begin{align*}\iint\limits_{S}{{40y\,dS}}& = \int_{0}^{{2\pi }}{{\int_{1}^{{73}}{{120\left( {\frac{1}{{72}}} \right)\left( {\frac{1}{{36}}} \right)\left( {u - 1} \right){u^{\frac{1}{2}}}\,du}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{1}^{{73}}{{\frac{5}{{108}}\left( {{u^{\frac{3}{2}}} - {u^{\frac{1}{2}}}} \right)\,du}}\,d\theta }}\end{align*}\]Note that we also converted the \(r\) limits in the original integral into \(u\) limits simply by plugging the “old” \(r\) limits into the substitution to get “new” \(u\) limits.
We can now easily finish evaluating the integral.
\[\begin{align*}\iint\limits_{S}{{40y\,dS}} & = \int_{0}^{{2\pi }}{{\left. {\frac{5}{{108}}\left( {\frac{2}{5}{u^{\frac{5}{2}}} - \frac{2}{3}{u^{\frac{3}{2}}}} \right)} \right|_1^{73}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\frac{5}{{108}}\left[ {\frac{2}{5}\left( {{{73}^{\frac{5}{2}}}} \right) - \frac{2}{3}\left( {{{73}^{\frac{3}{2}}}} \right) - \left( { - \frac{4}{{15}}} \right)} \right]\,d\theta }}\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{5\pi }}{{54}}\left[ {\frac{2}{5}\left( {{{73}^{\frac{5}{2}}}} \right) - \frac{2}{3}\left( {{{73}^{\frac{3}{2}}}} \right) + \frac{4}{{15}}} \right]\, = 5176.8958}}\end{align*}\]Kind of messy integral with a messy answer but that will happen on occasion so we shouldn’t get too excited about it when that does happen.