Section 17.3 : Surface Integrals
6. Evaluate \( \displaystyle \iint\limits_{S}{{x - z\,dS}}\) where \(S\) is the surface of the solid bounded by \({x^2} + {y^2} = 4\), \(z = x - 3\), and \(z = x + 2\). Note that all three surfaces of this solid are included in \(S\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
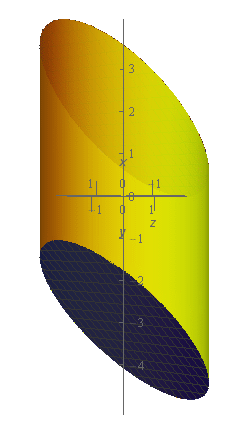
As noted in the problem statement there are three surfaces here. The “top” of the cylinder is a little hard to see. We made the walls of the cylinder slightly transparent and the top of the cylinder can be seen as a darker ellipse along the top of the surface.
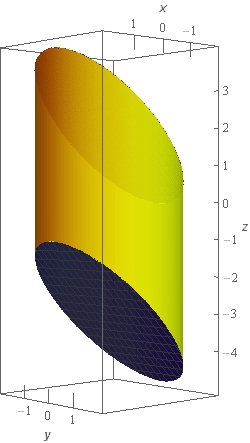
To help visualize the relationship between the top and bottom of the cylinder here is a different view of the surface.
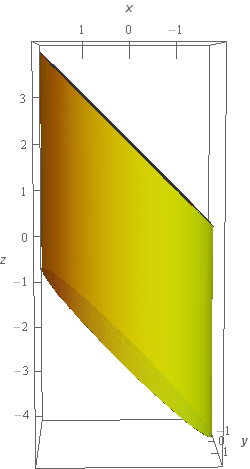
From this view we can see that the top and bottom planes that “cap” the cylinder are parallel.
Let’s define the three surfaces in the sketch as follows.
\({S_1}:{\mbox{ Cylinder given by }}{x^2} + {y^2} = 4\,\,\,\left( {i.e{\mbox{ the walls of the solid}}} \right)\)
\({S_2}:{\mbox{ Plane given by }}z = x + 2{\rm{ }}\left( {i.e{\mbox{ the top cap of the cylinder}}} \right)\)
\({S_3}:{\mbox{ Plane given by }}z = x - 3{\rm{ }}\left( {i.e{\mbox{ the bottom cap of the cylinder}}} \right)\)
Now we need to go through and do the integral for each of these surfaces and we’re going to go through these a little quicker than we did for the first few problems in this section.
Show Step 2Let’s start with \({S_1}\). The surface in this case is a cylinder and so we’ll need to parameterize it. The parameterization of the surface is,
\[\vec r\left( {z,\theta } \right) = \left\langle {2\cos \theta ,2\sin \theta ,z} \right\rangle \]The limits on \(z\) and \(\theta \) are,
\[0 \le \theta \le 2\pi ,\,\,\,\,\,2\cos \theta - 3 = x - 3 \le z \le x + 2 = 2\cos \theta + 2\]With the \(z\) limits we’ll need to make sure that we convert the \(x\)’s into their parameterized form.
In order to evaluate the integral in this case we’ll need the cross product \({\vec r_z} \times {\vec r_\theta }\) so here is that work.
\[{\vec r_z} = \left\langle {0,0,1} \right\rangle \hspace{0.25in}\hspace{0.25in}{\vec r_\theta } = \left\langle { - 2\sin \theta ,2\cos \theta ,0} \right\rangle \] \[{\vec r_z} \times {\vec r_\theta } = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\0&0&1\\{ - 2\sin \theta }&{2\cos \theta }&0\end{array}} \right| = - 2\cos \theta \vec i - 2\sin \theta \vec j\]Next, we’ll need the magnitude of the cross product so here is that.
\[\left\| {{{\vec r}_z} \times {{\vec r}_\theta }} \right\| = \sqrt {4{{\cos }^2}\theta + 4{{\sin }^2}\theta } = 2\]The integral in this case is,
\[\iint\limits_{{{S_1}}}{{x - z\,dS}} = \iint\limits_{D}{{\left[ {2\cos \theta - z} \right]\left( 2 \right)\,dA}} = \iint\limits_{D}{{4\cos \theta - 2z\,dA}}\]Don’t forget to plug the parameterization of the surface into the integrand and don’t forget to add in the magnitude of the cross product!
Now, \(D\) for this surface is nothing more than the limits on \(z\) and \(\theta \) we gave above.
Now let’s compute the integral for this surface.
\[\begin{align*}\iint\limits_{{{S_1}}}{{x - z\,dS}} & = \int_{0}^{{2\pi }}{{\int_{{2\cos \theta - 3}}^{{2\cos \theta + 2}}{{4\cos \theta - 2z\,dz}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\left. {\left( {4z\cos \theta - {z^2}} \right)} \right|_{2\cos \theta - 3}^{2\cos \theta + 2}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{4\cos \theta \left[ {2\cos \theta + 2 - \left( {2\cos \theta - 3} \right)} \right] - \left[ {{{\left( {2\cos \theta + 2} \right)}^2} - {{\left( {2\cos \theta - 3} \right)}^2}} \right]\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{5\,d\theta }} = \underline {10\pi } \end{align*}\]Do not forget to simplify! As we saw with this problem after the \(z\) integration the integrand looked really messy but after some pretty simple simplification it reduced down to an incredibly simple integrand.
Show Step 3Next we’ll take care of \({S_2}\). In this case the equation for the surface is simply \(z = x + 2\) and \(D\) is the disk \({x^2} + {y^2} \le 4\).
The integral in this case is,
\[\iint\limits_{{{S_2}}}{{x - z\,dS}} = \iint\limits_{D}{{\left[ {x - \left( {x + 2} \right)} \right]\sqrt {{{\left( 1 \right)}^2} + {{\left( 0 \right)}^2} + 1} \,dA}} = \iint\limits_{D}{{ - 2\sqrt 2 \,dA}} = - 2\sqrt 2 \iint\limits_{D}{{dA}}\]Okay, in this case we don’t need to actually do the evaluation of the integral because we know that,
\[\iint\limits_{D}{{dA}} = {\mbox{Area of }}D\]and in this case \(D\) is just a disk and we can quickly determine its area without any evaluation.
So, the integral for this surface is then just,
\[\iint\limits_{{{S_2}}}{{x - z\,dS}} = - 2\sqrt 2 \left( {{\mbox{Area of }}D} \right) = - 2\sqrt 2 \left[ {{{\left( 2 \right)}^2}\pi } \right] = \underline { - 8\sqrt 2 \pi } \] Show Step 4Finally, let’s integrate over \({S_3}\). In this case the equation for the surface is simply \(z = x - 3\) and \(D\) is the disk \({x^2} + {y^2} \le 4\).
The integral in this case is,
\[\begin{align*}\iint\limits_{{{S_3}}}{{x - z\,dS}} & = \iint\limits_{D}{{\left[ {x - \left( {x - 3} \right)} \right]\sqrt {{{\left( 1 \right)}^2} + {{\left( 0 \right)}^2} + 1} \,dA}}\\ & = \iint\limits_{D}{{3\sqrt 2 \,dA}} = 3\sqrt 2 \iint\limits_{D}{{dA}} = 3\sqrt 2 \left( {4\pi } \right) = \underline {12\sqrt 2 \pi } \end{align*}\]So, the integral in this case ended up being every similar to the integral in Step 3 and so we didn’t put in any of the explanation here.
Show Step 5Now, to get the value of the integral over the full surface all we need to do is sum up the values of each of the integrals over the three surfaces above. Doing this gives,
\[\iint\limits_{S}{{x - z\,dS}} = \left( {10\pi } \right) + \left( { - 8\sqrt 2 \pi } \right) + \left( {12\sqrt 2 \pi } \right) = \left( {10 + 4\sqrt 2 } \right)\pi = \require{bbox} \bbox[2pt,border:1px solid black]{{49.1875}}\]We put parenthesis around each of the individual integral values just to indicate where each came from. In general, these aren’t needed of course.