Section 15.6 : Triple Integrals in Cylindrical Coordinates
3. Evaluate \(\displaystyle \iiint\limits_{E}{{z\,dV}}\) where \(E\) is the region between the two planes \(x + y + z = 2\) and \(x = 0\) and inside the cylinder \({y^2} + {z^2} = 1\).
Show All Steps Hide All Steps
Start SolutionOkay, let’s start off with a quick sketch of the region \(E\) so we can get a feel for what we’re dealing with.
Let’s start off with a quick sketch of the cylinder and the plane \(x + y + z = 2\).

The region \(E\) we’re working with here is inside the cylinder and between the two planes given in the problem statement. What this basically means is that the two planes will cap the cylinder.
In the graph above we put in more of the cylinder than needed and more of the plane \(x + y + z = 2\) than needed just to help illustrate the relation between the two surfaces. The plane \(x = 0\) is just the \(yz\)-plane and “caps” the back of the cylinder and so isn’t included in the sketch.
Now, let’s get rid of the portion of the cylinder that is in front of \(x + y + z = 2\) since it’s not part of the region and let’s get rid of the portion of \(x + y + z = 2\) that is not inside the cylinder. The resulting sketch is the region \(E\).
Here then is the sketch of \(E\).
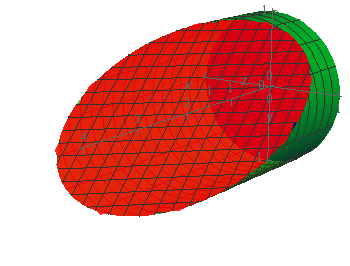
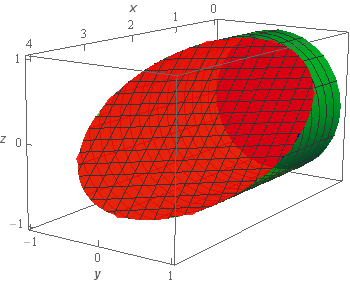
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface and region.
Show Step 2So, from the sketch it is hopefully clear that the region \(D\) will be in the \(yz\)-plane and so we’ll need to integrate with respect to \(x\) first. That means that the \(x\) limits are,
\[0 \le x \le 2 - y - z\]For the upper \(x\) limit all we need to do is solve the equation of the plane for \(x\).
Show Step 3For this problem \(D\) is simply the disk \({y^2} + {z^2} \le 1\). Because \(D\) is in the \(yz\)-plane and is a disk we’ll need to use the following “modified” version of cylindrical coordinates.
\[\begin{align*}x & = x\\ y & = r\sin \theta \\ z & = r\cos \theta \end{align*}\]This also matches up with the fact that we need to integrate \(x\) first (as we determined in Step 2) and the first variable of integration with cylindrical coordinates is always the “free” variable (i.e. not the one involving the trig functions).
So, we can easily describe the disk in terms of \(r\) and \(\theta \) so here are the cylindrical coordinates for this problem.
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le 1\\ 0 \le x \le 2 - r\sin \theta - r\cos \theta \end{array}\]Don’t forget to convert the \(y\) and \(z\) in the \(x\) upper limit into cylindrical coordinate as well.
Show Step 4Plugging these limits into the integral and converting to cylindrical coordinates gives,
\[\begin{align*}\iiint\limits_{E}{{z\,dV}}& = \int_{0}^{{2\pi }}{{\int_{0}^{1}{{\int_{0}^{{2 - r\sin \theta - r\cos \theta }}{{\left( {r\cos \theta } \right)r\,dx}}\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{1}{{\int_{0}^{{2 - r\sin \theta - r\cos \theta }}{{{r^2}\cos \theta \,dx}}\,dr}}\,d\theta }}\end{align*}\]Don’t forget to convert the integrand to our modified cylindrical coordinates and also don’t forget that \(dV = r\,dx\,dr\,d\theta \) and so we pick up another \(r\) when converting the \(dV\) to cylindrical coordinates.
Show Step 5Okay, now all we need to do is evaluate the integral. Here is the \(x\) integration.
\[\begin{align*}\iiint\limits_{E}{{z\,dV}} & = \int_{0}^{{2\pi }}{{\int_{0}^{1}{{\left. {\left( {{r^2}\cos \theta \,x} \right)} \right|_0^{2 - r\sin \theta - r\cos \theta }\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{1}{{{r^2}\cos \theta \,\left( {2 - r\sin \theta - r\cos \theta } \right)\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{1}{{2{r^2}\cos \theta - {r^3}\cos \theta \sin \theta - {r^3}{{\cos }^2}\theta \,dr}}\,d\theta }}\end{align*}\] Show Step 6Next let’s do the \(r\) integration.
\[\begin{align*}\iiint\limits_{E}{{z\,dV}} & = \int_{0}^{{2\pi }}{{\left. {\left( {\frac{2}{3}{r^3}\cos \theta - \frac{1}{4}{r^4}\cos \theta \sin \theta - \frac{1}{4}{r^4}{{\cos }^2}\theta } \right)} \right|_0^1\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\frac{2}{3}\cos \theta - \frac{1}{4}\cos \theta \sin \theta - \frac{1}{4}{{\cos }^2}\theta \,d\theta }}\end{align*}\] Show Step 7Finally, we’ll do the \(\theta \) integration.
\[\begin{align*}\iiint\limits_{E}{{z\,dV}} & = \int_{0}^{{2\pi }}{{\frac{2}{3}\cos \theta - \frac{1}{8}\sin \left( {2\theta } \right) - \frac{1}{8}\left( {1 + \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \left. {\left( {\frac{2}{3}\sin \theta + \frac{1}{{16}}\cos \left( {2\theta } \right) - \frac{1}{8}\left( {\theta + \frac{1}{2}\sin \left( {2\theta } \right)} \right)} \right)} \right|_0^{2\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{\pi }{4}}}\end{align*}\]Don’t forget to simplify the integrand before doing the final integration. In this case we used the sine double angle on the second term and the cosine half angle formula on the third term to simplify the integrand to allow us to quickly do this integration.