Section 15.5 : Triple Integrals
5. Evaluate \( \displaystyle \iiint\limits_{E}{{12y - 8x\,dV}}\) where \(E\) is the region behind \(y = 10 - 2z\) and in front of the region in the \(xz\)-plane bounded by \(z = 2x\), \(z = 5\) and \(x = 0\).
Show All Steps Hide All Steps
Start SolutionOkay, let’s start off with a quick sketch of the region \(E\) so we can get a feel for what we’re dealing with.
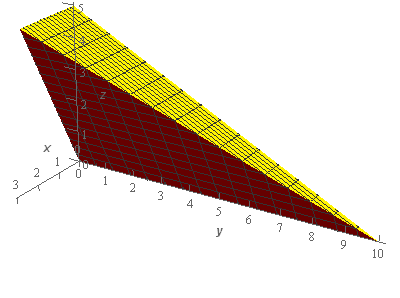
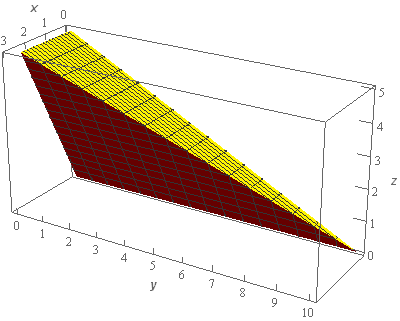
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface and region.
The top portion of the region (the yellow colored surface) is the graph of the portion \(y = 10 - 2z\) that lies in front of the region \(xz\)-plane given in the problem statement.
The red surface is the plane defined by \(z = 2x\). This is the plane that intersects the \(xz\)‑plane at the line \(z = 2x\) and is bounded above by the surface \(y = 10 - 2z\).
Show Step 2The region in the \(xz\)-plane bounded by \(z = 2x\), \(z = 5\) and \(x = 0\) that is referenced in the problem statement is the region \(D\) and so we know that, for this problem, we’ll need to be integrating \(y\) first (since \(D\) is in the \(xz\)-plane).
Therefore, we have the following limits for \(y\).
\[0 \le y \le 10 - 2z\]With these limits we can also get the triple integral at least partially set up as follows.
\[\iiint\limits_{E}{{12y - 8x\,dV}} = \iint\limits_{D}{{\left[ {\int_{0}^{{10 - 2z}}{{12y - 8x\,dy}}} \right]\,dA}}\] Show Step 3Next, we’ll need limits for \(D\) so we can finish setting up the integral. For this problem \(D\) is the region in the \(xz\)-plane from the problem statement as we noted above.
Here is a quick sketch of \(D\).
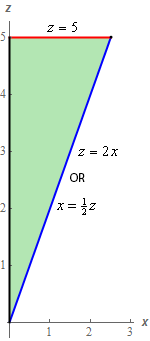
Another way to think this region is that it is the “back” of the solid sketched in Step 1 and the solid we sketched in Step 1 is all behind this region. In other words the positive y‑axis is goes directly back into the page while the negative \(y\)-axis comes directly out of the page.
As noted in the sketch of \(D\) we can easily defined by either of the following sets of limits.
\[\begin{array}{*{20}{c}}\begin{aligned}& \,\,\,0 \le x \le \frac{5}{2}\\ & 2x \le z \le 5\end{aligned}&{\,\,\,\,\,\,\,\,\,\,\,{\mbox{OR}}\,\,\,\,\,\,\,\,\,\,}&\begin{aligned} & \,\, 0 \le z \le 5\\ & 0 \le x \le \frac{1}{2}z\end{aligned}\end{array}\]The integrand doesn’t really suggest one of these would be easier than the other so we’ll use the 2nd set of limits for no other reason than the lower limits for both are zero which might make things a little nicer in the integration process.
With these limits plugged into the integral we now have,
\[\iiint\limits_{E}{{12y - 8x\,dV}} = \int_{0}^{5}{{\int_{0}^{{\frac{1}{2}z}}{{\int_{0}^{{10 - 2z}}{{12y - 8x\,dy}}\,dx}}\,dz}}\] Show Step 4Okay, now all we need to do is evaluate the integral. Here is the \(y\) integration.
\[\begin{align*}\iiint\limits_{E}{{12y - 8x\,dV}} & = \int_{0}^{5}{{\int_{0}^{{\frac{1}{2}z}}{{\left. {\left( {6{y^2} - 8xy} \right)} \right|_0^{10 - 2z}\,dx}}\,dz}}\\ & = \int_{0}^{5}{{\int_{0}^{{\frac{1}{2}z}}{{6{{\left( {10 - 2z} \right)}^2} - 8x\left( {10 - 2z} \right)\,dx}}\,dz}}\end{align*}\]Note that we did no simplification here because it is not yet clear that we need to do any simplification. The next integration is with respect to \(x\) and the first term is a constant as far as that integration is concerned and the second term is multiplied by an \(x\) and so it will might well be easier to leave it in that form for the \(x\) integration.
Show Step 5Now let’s do the \(x\) integration.
\[\begin{align*}\iiint\limits_{E}{{12y - 8x\,dV}} & = \int_{0}^{5}{{\left. {\left[ {6{{\left( {10 - 2z} \right)}^2}x - 4{x^2}\left( {10 - 2z} \right)} \right]} \right|_0^{\frac{1}{2}z}\,dz}}\\ & = \int_{0}^{5}{{3z{{\left( {10 - 2z} \right)}^2} - {z^2}\left( {10 - 2z} \right)\,dz}}\\ & = \int_{0}^{5}{{14{z^3} - 130{z^2} + 300z\,dz}}\end{align*}\] Show Step 6Finally, let’s do the \(z\) integration.
\[\iiint\limits_{E}{{12y - 8x\,dV}} = \left. {\left( {\frac{7}{2}{z^4} - \frac{{130}}{3}{z^3} + 150{z^2}} \right)} \right|_0^5 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{3125}}{6}}}\]So, once we got the limits all set up, the integration for this problem wasn’t too bad. That will often be the case with these problems. Getting the limits for the integrals set up will often, but not always, be the hardest part of the problem. Once they get set up the integration is often pretty simple.