Calculus III - Triple Integrals

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 15.5 : Triple Integrals

Back to Problem List

9. Use a triple integral to determine the volume of the region that is below $z = 8 - {x^2} - {y^2}$ above $z = - \sqrt {4{x^2} + 4{y^2}}$ and inside ${x^2} + {y^2} = 4$ .

Show All Steps Hide All Steps

Start Solution

Okay, let’s start off with a quick sketch of the region we want the volume of so we can get a feel for what we’re dealing with. We’ll call this region $E$ .

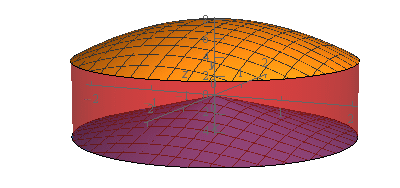
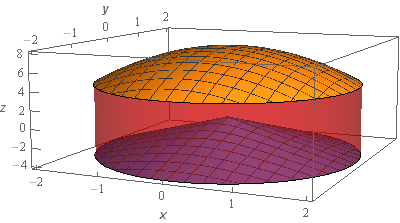
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface and region.

The top of the region (the orange colored surface) is the portion of the graph of the elliptic paraboloid $z = 8 - {x^2} - {y^2}$ that is inside the cylinder ${x^2} + {y^2} = 4$ . The bottom of the region is the portion of the graph of the cone $z = - \sqrt {4{x^2} + 4{y^2}}$ that is inside the cylinder ${x^2} + {y^2} = 4$ . The walls of the region (which are translucent to show the bottom portion) is the cylinder ${x^2} + {y^2} = 4$ .

Show Step 2

The volume of this solid is given by,

$V = \iiint\limits_{E}{{dV}}$ Show Step 3

So, we now need to get the limits set up for the integral. From the sketch above we can see that we’ll need to integrate with respect to z first so here are those limits.

$- \sqrt {4{x^2} + 4{y^2}} \le z \le 8 - {x^2} - {y^2}$

We’ll also need limits for $D$ . In this case $D$ is just the disk given by ${x^2} + {y^2} \le 4$ (i.e. the portion of the $xy$ -plane that is inside the cylinder. This is the region in the $xy$ -plane that we need to graph the paraboloid and cone and so is $D$ .

Because $D$ is a disk it makes sense to use polar coordinates for integrating over $D$ . Here are the limits for $D$ .

$\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le 2\end{array}$

Now, let’s set up the volume integral as follows.

$V = \iiint\limits_{E}{{dV}} = \iint\limits_{D}{{\left[ {\int_{{ - \sqrt {4{x^2} + 4{y^2}} }}^{{8 - {x^2} - {y^2}}}{{\,dz}}} \right]\,dA}}$

Because we know that we’ll need to do the outer double integral in polar coordinates we’ll hold off putting those limits in until we have the $z$ integration done.

Show Step 4

Okay, let’s do the $z$ integration.

$\begin{align*}V & = \iint\limits_{D}{{\left. z \right|_{ - \sqrt {4{x^2} + 4{y^2}} }^{8 - {x^2} - {y^2}}\,dA}}\\ & = \iint\limits_{D}{{8 - {x^2} - {y^2} + \sqrt {4{x^2} + 4{y^2}} \,dA}}\end{align*}$ Show Step 5

Now let’s convert the integral over to polar coordinates. Don’t forget that ${x^2} + {y^2} = {r^2}$ and that $dA = r\,dr\,d\theta$ .

The volume integral in terms of polar coordinates is then,

$\begin{align*}V & = \int_{0}^{{2\pi }}{{\int_{0}^{2}{{\left[ {8 - {r^2} + 2r} \right]r\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{2}{{8r - {r^3} + 2{r^2}\,dr}}\,d\theta }}\end{align*}$ Show Step 6

The $r$ integration is then,

$V = \int_{0}^{{2\pi }}{{\left. {\left( {4{r^2} - \frac{1}{4}{r^4} + \frac{2}{3}{r^3}} \right)} \right|_0^2\,d\theta }} = \int_{0}^{{2\pi }}{{\frac{{52}}{3}\,d\theta }}$ Show Step 7

Finally, we can compute the very simple $\theta$ integral to get the volume of the region.

$V = \int_{0}^{{2\pi }}{{\frac{{52}}{3}\,d\theta }} = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{104}}{3}\pi }}$