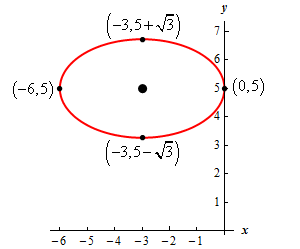Section 4.3 : Ellipses
1. Sketch the graph of the following ellipse.
\[\frac{{{{\left( {x + 3} \right)}^2}}}{9} + \frac{{{{\left( {y - 5} \right)}^2}}}{3} = 1\]Show All Steps Hide All Steps
Start SolutionThe first step here is to simply compare our equation to the standard form of the ellipse and identify all the important information. For reference purposes here is the standard form of the ellipse.
\[\frac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\] Comparing our equation to this we can see we have the following information. \[h = - 3\hspace{0.25in}k = 5\hspace{0.25in}a = 3\hspace{0.25in}b = \sqrt 3 \]Do, not worry about the square root in \(b\). There is no reason to expect any of the numbers in the denominator to be perfect squares. They often aren’t and so we need to be able to deal with them when they aren’t. When we do get roots showing up it just means a couple of the points will be decimals instead of “nice” integers like we usually see with these kinds of problems.
Show Step 2With the information we found in the first step we can see that the center of the ellipse is \(\left( { - 3,5} \right)\).
The right most, left most, top most and bottom most points are then,
\[\begin{align*}& {\mbox{Right Most Point :}}\,\,\left( {0,5} \right)\\ & {\mbox{Left Most Point :}}\,\,\left( { - 6,5} \right)\\ & {\mbox{Top Most Point :}}\,\,\left( { - 3,5 + \sqrt 3 } \right) = \left( { - 3,6.7321} \right)\\ & {\mbox{Bottom Most Point :}}\,\,\left( { - 3,5 - \sqrt 3 } \right) = \left( { - 3,3.2679} \right)\end{align*}\] Show Step 3Here is a sketch of the ellipse including all the points we found above.