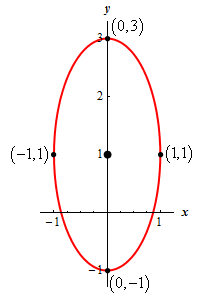Section 4.3 : Ellipses
2. Sketch the graph of the following ellipse.
\[{x^2} + \frac{{{{\left( {y - 1} \right)}^2}}}{4} = 1\]Show All Steps Hide All Steps
Start SolutionThe first step here is to simply compare our equation to the standard form of the ellipse and identify all the important information. For reference purposes here is the standard form of the ellipse.
\[\frac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\]To help with the comparison let’s rewrite our equation a little to make it look more like the standard form.
\[\frac{{{{\left( {x - 0} \right)}^2}}}{1} + \frac{{{{\left( {y - 1} \right)}^2}}}{4} = 1\]We don’t really need the “1” in the denominator nor do we need the “-0” in the numerator of the first term, but it might help to with the comparison process.
Comparing our equation to this we can see we have the following information. \[h = 0\hspace{0.25in}k = 1\hspace{0.25in}a = 1\hspace{0.25in}b = 2\] Show Step 2With the information we found in the first step we can see that the center of the ellipse is \(\left( {0,1} \right)\).
The right most, left most, top most and bottom most points are then,
\[\begin{align*} & {\mbox{Right Most Point :}}\,\,\left( {1,1} \right)\\ & {\mbox{Left Most Point :}}\,\,\left( { - 1,1} \right)\\ & {\mbox{Top Most Point :}}\,\,\left( {0,3} \right)\\ & {\mbox{Bottom Most Point :}}\,\,\left( {0, - 1} \right)\end{align*}\] Show Step 3Here is a sketch of the ellipse including all the points we found above.