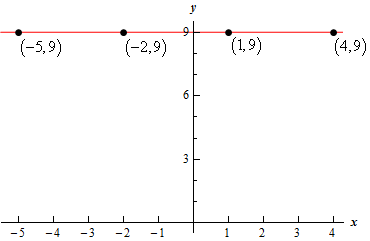Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 3.5 : Graphing Functions
3. Construct a table of at least 4 ordered pairs of points on the graph of the following function and use the ordered pairs from the table to sketch the graph of the function.
\[f\left( x \right) = 9\]Show All Steps Hide All Steps
Hint : Do not get excited about the lack of \(x\)’s on the right side. This function evaluates just like all the functions you’ve evaluated.
This is a constant function. The fact that there are no \(x\)’s on the right side is not a problem. Here is the table of points we’ll use for this problem.
| \(x\) | \(f\left( x \right)\) | \(\left( {x,y} \right)\) |
|---|---|---|
| -5 | 9 | \(\left( { - 5,9} \right)\) |
| -2 | 9 | \(\left( { - 2,9} \right)\) |
| 1 | 9 | \(\left( {1,9} \right)\) |
| 4 | 9 | \(\left( {4,9} \right)\) |
Because there are no \(x\)’s on the right side there are no \(x\)’s to plug numbers in. That in turn means that no matter what \(x\) we plug into the function we always get a function value of 9 as our table above shows.
Show Step 2Here is a sketch of the function.