Section 3.5 : Graphing Functions
5. Construct a table of at least 4 ordered pairs of points on the graph of the following function and use the ordered pairs from the table to sketch the graph of the function.
\[f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{5 + x}&{{\mbox{if }}x \ge 1}\\2&{{\mbox{if }} - 2 \le x < 1}\\{1 - {x^2}}&{{\mbox{if }}x < - 2}\end{array}} \right.\]Show All Steps Hide All Steps
We have a piecewise function here so we need to make sure and pick points from each range of \(x\) when building our table of points. Also, we’ll want to plug the “cutoff points”, \(x = - 2\) and \(x = 1\) , into the corresponding equation as well so we know where each will be at the end of the range of \(x\)’s for which it is valid.
Here is the table of points we’ll use for this problem.
| \(x\) | \(1 - {x^2}\) | \(\left( {x,y} \right)\) |
|---|---|---|
| -4 | -15 | \(\left( { - 4, - 15} \right)\) |
| -3 | -8 | \(\left( { - 3, - 8} \right)\) |
| -2 | -3 | \(\left( { - 2, - 3} \right)\) |
| \(x\) | 2 | \(\left( {x,y} \right)\) |
|---|---|---|
| -2 | 2 | \(\left( { - 2,2} \right)\) |
| -1 | 2 | \(\left( { - 1,2} \right)\) |
| 1 | 2 | \(\left( {1,2} \right)\) |
| \(x\) | \(5 + x\) | \(\left( {x,y} \right)\) |
|---|---|---|
| 1 | 6 | \(\left( {1,6} \right)\) |
| 2 | 7 | \(\left( {2,7} \right)\) |
| 3 | 8 | \(\left( {3,8} \right)\) |
Here is a sketch of the function.
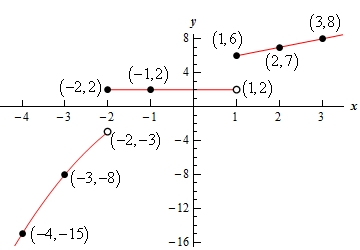
In this case neither of the pieces of the graph met at the cutoff points. This is the reason we compute the value of each equation at the cutoff points. Without doing that we wouldn’t know if they met at the cutoff point or not.