Algebra - Rational Functions

Show Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 4.8 : Rational Functions

Back to Problem List

1. Sketch the graph of the following function. Clearly identify all intercepts and asymptotes.

$f\left( x \right) = \frac{{ - 4}}{{x - 2}}$

Show All Steps Hide All Steps

Start Solution

Let’s first find the intercepts for this function.

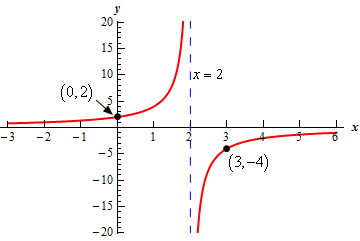
The $y$ -intercept is the point $\left( {0,f\left( 0 \right)} \right) = \left( {0,2} \right)$ .

For the $x$ -intercepts we set the numerator equal to zero and solve. However, in this case the numerator is a constant (-4 specifically) and so can’t ever be zero. Therefore, this function will have no $x$ -intercepts.

Show Step 2

We can find any vertical asymptotes be setting the denominator equal to zero and solving. Doing that for this function gives,

$x - 2 = 0\hspace{0.25in} \to \hspace{0.25in}x = 2$

So, we’ll have a vertical asymptote at $x = 2$ .

Show Step 3

For this equation the largest exponent of $x$ in the numerator is zero since the numerator is a constant. The largest exponent of $x$ in the denominator is 1, which is larger than the largest exponent in the numerator, and so the $x$ -axis will be the horizontal asymptote.

Show Step 4

From Step 2 we saw we only have one vertical asymptote and so we only have two regions to our graph : $x < 2$ and $x > 2$ .

We’ll need a point in each region to determine if it will be above or below the horizontal asymptote. Here are a couple of function evaluations for the points.

$\begin{align*}f\left( 0 \right) & = 2 & \to \hspace{0.25in} & \left( {0,2} \right)\\ f\left( 3 \right) & = - 4 & \to \hspace{0.25in} & \left( {3, - 4} \right)\end{align*}$

Note that the first evaluation didn’t really need to be done since it was just the $y$ -intercept which we had already found in the first step. It was included here mostly for the sake of completeness.

Show Step 5

Here is a sketch of the function with the points found above. The vertical asymptote is indicated with a blue dashed line and recall that the horizontal asymptote is just the $x$ -axis.