Algebra - Applications of Linear Equations

Show Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 2.3 : Applications of Linear Equations

Back to Problem List

3. Two planes start out 2800 km apart and move towards each other meeting after 3.5 hours. One plane flies at 75 km/hour slower than the other plane. What was the speed of each plane?

Show All Steps Hide All Steps

Start Solution

Let’s start with a diagram of what is going on in this situation.

Show Step 2

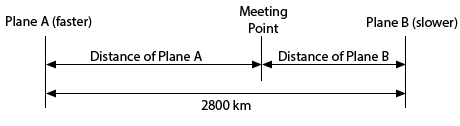
We can next set up a word equation for this situation.

$\left( \begin{array}{c}{\mbox{Distance}}\\ {\mbox{of Plane A}}\end{array} \right) + \left( \begin{array}{c}{\mbox{Distance}}\\ {\mbox{of Plane B}}\end{array} \right) = 2800$

We know that Distance = Rate X Time so this gives to following word equation.

$\left( \begin{array}{c}{\mbox{Rate of}}\\ {\mbox{Plane A}}\end{array} \right)\left( \begin{array}{c}{\mbox{Time of}}\\ {\mbox{Plane A}}\end{array} \right) + \left( \begin{array}{c}{\mbox{Rate of}}\\ {\mbox{Plane B}}\end{array} \right)\left( \begin{array}{c}{\mbox{Time of}}\\ {\mbox{Plane B}}\end{array} \right) = 2800$ Show Step 3

Let’s let $r$ be the speed of the faster plane. Therefore, the speed of the slower plane is $r - 75$ . We also know that each plane travels for 3.5 hours. Plugging all this information into the word equation above gives the following equation.

$\begin{align*}\left( r \right)\left( {3.5} \right) + \left( {r - 75} \right)\left( {3.5} \right) & = 2800\\ 3.5r + 3.5\left( {r - 75} \right) & = 2800\end{align*}$ Show Step 4

Now we can solve this equation for the speed of the faster plane.

$\begin{align*}3.5r + 3.5\left( {r - 75} \right) & = 2800\\ 7r - 262.5 & = 2800\\ 7r & = 3062.5\\ r & = 437.5\end{align*}$

So, the faster plane is traveling at 437.5 km/hour while the slower plane is traveling at 362.5 km/hour (75 km/hour slower than faster plane).