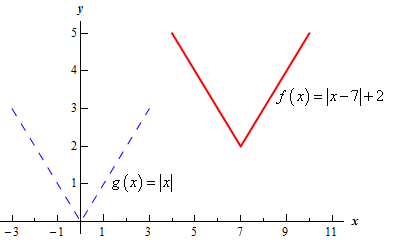Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 4.6 : Transformations
7. Use transformations to sketch the graph of the following function.
\[f\left( x \right) = \left| {x - 7} \right| + 2\]Show All Steps Hide All Steps
Start SolutionLet’s first identify the “base” function (i.e. the function we are transforming). In this case it looks like we are transforming \(g\left( x \right) = \left| x \right|\) .
Show Step 2The function that have here looks like it can be written as,
\[f\left( x \right) = \left| {x - 7} \right| + 2 = g\left( {x - 7} \right) + 2\]Therefore, we can see that the graph of \(f\left( x \right)\) is simply going to be the graph of \(g\left( x \right)\) shifted right by 7 and up by 2.
Show Step 3Here is a sketch of both the base function (blue dashed curve) and the function we were asked to graph (red solid curve).