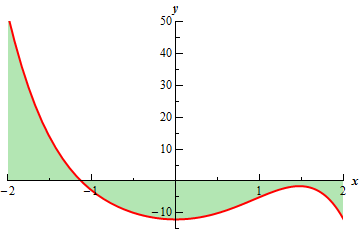Section 5.5 : Area Problem
4. Estimate the net area between \(f\left( x \right) = 8{x^2} - {x^5} - 12\) and the \(x\)-axis on \(\left[ { - 2,2} \right]\) using \(n = 8\) and the midpoints of the subintervals for the height of the rectangles. Without looking at a graph of the function on the interval does it appear that more of the area is above or below the \(x\)-axis?
Show All Steps Hide All Steps
Start SolutionFirst let’s estimate the area between the function and the \(x\)-axis on the interval. The widths of each of the subintervals for this problem are,
\[\Delta x = \frac{{2 - \left( { - 2} \right)}}{8} = \frac{1}{2}\]We don’t need to actually graph the function to do this problem. It would probably help to have a number line showing subintervals however. Here is that number line.
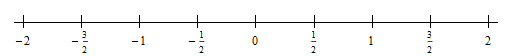
Now, we’ll be using midpoints of each of these subintervals to determine the height of each of the rectangles.
The area between the function and the \(x\)-axis is then approximately,
\[{\mbox{Area}} \approx \frac{1}{2}f\left( { - \frac{7}{4}} \right) + \frac{1}{2}f\left( { - \frac{5}{4}} \right) + \frac{1}{2}f\left( { - \frac{3}{4}} \right) + \frac{1}{2}f\left( { - \frac{1}{4}} \right) + \frac{1}{2}f\left( {\frac{1}{4}} \right) + \frac{1}{2}f\left( {\frac{3}{4}} \right) + \frac{1}{2}f\left( {\frac{5}{4}} \right) + \frac{1}{2}f\left( {\frac{7}{4}} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 6}}\]We’ll leave it to you to check all the function evaluations. They get a little messy, but after all the arithmetic is done we get a net area of -6.
Show Step 2Now, as we (hopefully) recall from the discussion in this section area above the \(x\)-axis is positive and area below the \(x\)-axis is negative. In this case we have estimated that the net area is -6 and so, assuming that our estimate is accurate, it looks like we should have more area is below the \(x\)-axis as above it.
For reference purposes here is the graph of the function with the area shaded in and as we can see it does appear that there is slightly more area below as above the \(x\)-axis.