Section 3.9 : Chain Rule
30. The position of an object is given by \(s\left( t \right) = \sin \left( {3t} \right) - 2t + 4\). Determine where in the interval \(\left[ {0,3} \right]\) the object is moving to the right and moving to the left.
Show All Steps Hide All Steps
Start SolutionWe’ll first need the derivative because we know that the derivative will give us the velocity of the object. Here is the derivative.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{s'\left( t \right) = 3\cos \left( {3t} \right) - 2}}\] Show Step 2Next, we need to know where the object stops moving and so all we need to do is set the derivative equal to zero and solve.
\[3\cos \left( {3t} \right) - 2 = 0\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}\cos \left( {3t} \right) = \frac{2}{3}\]A quick calculator computation tells us that,
\[3t = {\cos ^{ - 1}}\left( {\frac{2}{3}} \right) = 0.8411\]Recalling our work in the Review chapter and a quick check on a unit circle we can see that either \(3t = 0.8411\) or \(3t = 2\pi - 0.8411 = 5.4421\) can be used for the second angle. Note that either will work, but we’ll use the second simply because it is the positive angle.
Putting all of this together and dividing by 3 we can see that the derivative will be zero at,
\[\begin{align*}3t & = 0.8411 + 2\pi n\hspace{0.25in}{\mbox{and}}\hspace{0.25in}3t = 5.4421 + 2\pi n\hspace{0.25in}n = 0, \pm 1, \pm 2, \pm 3, \ldots \\ t & = 0.2804 + \frac{{2\pi n}}{3}\hspace{0.25in}{\mbox{and}}\hspace{0.25in}t = 1.8140 + \frac{{2\pi n}}{3}\hspace{0.25in}n = 0, \pm 1, \pm 2, \pm 3, \ldots \end{align*}\]Finally, all we need to do is plug in some \(n\)’s to determine which solutions fall in the interval we are working on, \(\left[ {0,3} \right]\).
So, in the interval \(\left[ {0,3} \right]\), the object stops moving at the following three points.
\[t = 0.2804,\,\,\,\,\,1.8140,\,\,\,\,2.3748\] Show Step 3To get the answer to this problem all we need to know is where the derivative is positive (and hence the object is moving to the right) or negative (and hence the object is moving to the left). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.
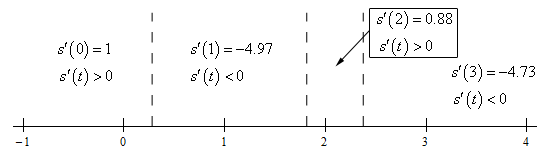
From this we get the following moving right/moving left information.
\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{array}{ll}{\mbox{Moving Right :}} & \,\,0 \le t < 0.2804,\,\,\,\,1.8140 < t < 2.3748\\ {\mbox{Moving Left :}} & \,\,0.2804 < t < 1.8140,\,\,\,\,2.3748 < t \le 3\end{array}}\]Note that because we’ve only looked at what is happening in the interval \(\left[ {0,3} \right]\) we can’t say anything about the moving right/moving left behavior of the object outside of this interval.