Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 1.10 : Common Graphs
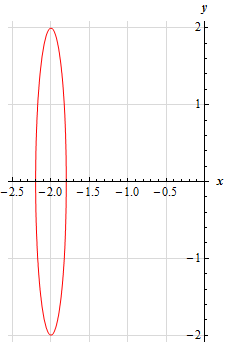
15. Without using a graphing calculator sketch the graph of \(\displaystyle 25{\left( {x + 2} \right)^2} + \frac{{{y^2}}}{{4}} = 1\).
Show SolutionThis is just an ellipse that is almost in standard form. With a little rewrite we can put it into standard form as follows,
\[\frac{{{\left( x+2 \right)}^{2}}}{{}^{1}/{}_{25}}+\frac{{{y}^{2}}}{4}=1\]We can now see that the ellipse has a center of \(\left( { - 2,0} \right)\) while the left/right most points will be \(\frac{1}{5} = 0.2\) units away from the center and the top/bottom most points will be 2 units away from the center. Here is a quick sketch of the ellipse.