Section 1.10 : Common Graphs
8. Without using a graphing calculator sketch the graph of \(f\left( y \right) = {\left( {y - 1} \right)^2} + 2\).
Even though our function is in the form \(x = f\left( y \right)\) we can still use the Algebraic transformations to help us sketch this graph. We do need to be careful however and remember that we’re working with interchanged variables and so the transformations will also switch.
In this case if we know the graph of \(h\left( y \right)\) then the graph of \(h\left( {y + c} \right) + k\) is simply the graph of \(h\left( x \right)\) shifted up by \(c\) units if \(c < 0\) or shifted down by \(c\) units if \(c > 0\) and shifted right by \(k\) units if \(k > 0\) or shifted left by \(k\) units if \(k < 0\).
So, in our case if \(h\left( y \right) = {y^2}\) we can see that,
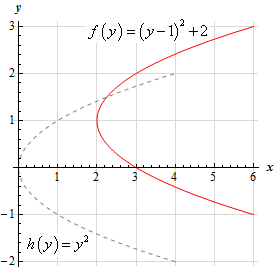
\[f\left( y \right) = {\left( {y - 1} \right)^2} + 2 = h\left( {y - 1} \right) + 2\]and so the graph we’re being asked to sketch is the graph of \(h\left( y \right) = {y^2}\) shifted up by 1 units and right by 2 units.
Here is the graph of \(f\left( y \right) = {\left( {y - 1} \right)^2} + 2\) and note that to help see the transformation we have also sketched in the graph of \(h\left( y \right) = {y^2}\).