Calculus I - Definition of the Definite Integral

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 5.6 : Definition of the Definite Integral

Back to Problem List

8. For \( \displaystyle \int_{1}^{4}{{3x - 2\,dx}}\) sketch the graph of the integrand and use the area interpretation of the definite integral to determine the value of the integral.

Show All Steps Hide All Steps

Start Solution

Here is the graph of the integrand, \(f\left( x \right) = 3x - 2\), on the interval \(\left[ {1,4} \right]\).

Show Step 2

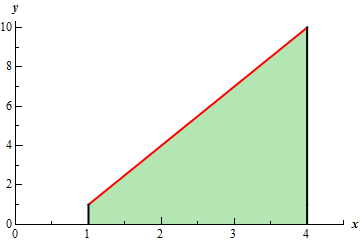
Now, we know that the integral is simply the area between the line and the \(x\)-axis and so we should be able to use basic area formulas to help us determine the value of the integral. Here is a “modified” graph that will help with this.

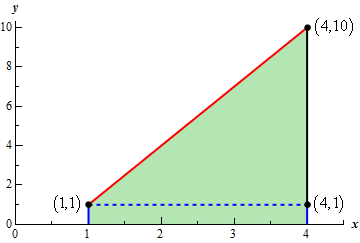
From this sketch we can see that we can think of this area as a rectangle with width 3 and height 1 and a triangle with base 3 and height 9. The value of the integral will then be the sum of the areas of the rectangle and the triangle.

Here is the value of the integral,

\[\int_{1}^{4}{{3x - 2\,dx}} = \left( 3 \right)\left( 1 \right) + \frac{1}{2}\left( 3 \right)\left( 9 \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{33}}{2}}}\]