Section 6.5 : More Volume Problems
1. Find the volume of a pyramid of height \(h\) whose base is an equilateral triangle of length \(L\).
Show All Steps Hide All Steps
Okay, let’s start with a sketch of the pyramid. These can be difficult to sketch but having the sketch will help greatly with the set up portion of the problem.
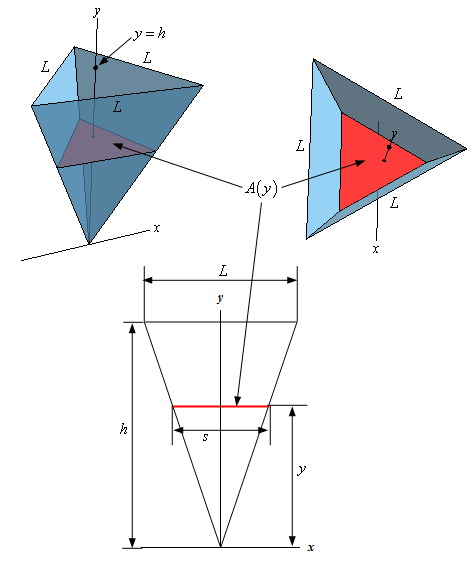
We’ve got several sketches here. In each sketch we’ve shown a representative cross‑sectional area (shown in red). Because the cross-section can be placed at any point on the \(y\)-axis the area of the cross-section will be a function of \(y\) as indicated in the image.
The sketch in the upper right we see the pyramid from the “front” and the sketch in the upper left we see pyramid from the “top”. Note that we set the point of the pyramid at the origin and drew the pyramid upwards. This was done to make the set up for the problem a little easier. Also we sketched the pyramid so that one of the sides of the pyramid was parallel to the \(x\)-axis. This was done only so we could draw in the bottom sketch (which we’ll get to in a second) and have the images match up, so to speak.
The bottom sketch is a sketch of the side of the pyramid that is parallel to the \(x\)-axis. It also has all of the various quantities that we’ll need shown. The representative cross-section here is indicated by the red line on the sketch.
Let’s start off with a sketch of what a typical cross-section looks like.
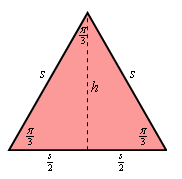
In this case we know that the cross-sections are equilateral triangles and so all of the interior angles are \(\frac{\pi }{3}\) and we know that all the sides are the same length, let’s say \(s\). In the sketch above notice that since we have an equilateral triangle we know that the dashed line (representing the height of the triangle) will divide the base of the triangle into equal length portions, i.e. \(\frac{s}{2}\). Also, from basic right triangle trig (each “half” of the cross-section is a right triangle right?) we can see that we can write the height in terms of \(s\) as follows,
\[\tan \left( {\frac{\pi }{3}} \right) = \frac{h}{{{}^{s}/{}_{2}}}\hspace{0.5in} \Rightarrow \hspace{0.5in} h = \frac{s}{2}\tan \left( {\frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}s\]Therefore, in terms of \(s\) the area of each cross-section is,
\[{\mbox{Area}} = \frac{1}{2}\left( s \right)\left( {\frac{{\sqrt 3 }}{2}s} \right) = \frac{{\sqrt 3 }}{4}{s^2}\]Now, we know from the sketches in Step 1 that the cross-sectional area should be a function of \(y\). So, if we could determine a relationship between \(s\) and \(y\) we’d have what we need. Let’s revisit one of the sketches from Step 1.
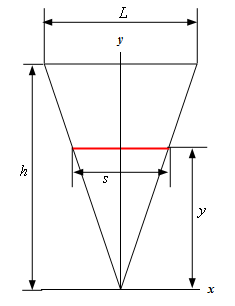
From this we can see that we have two similar triangles. The overall side (base \(L\) and height \(h\)) as well as the “lower” portion formed by the red line representing the cross‑sectional area (base \(s\) and height \(y\)).
Because these two triangles are similar triangles we know the following ratios must be equal.
\[\frac{s}{y} = \frac{L}{h}\hspace{0.5in} \Rightarrow \hspace{0.5in} s = \frac{L}{h}y\]We now have a relationship between \(s\) and \(y\) so plug this into the area formula from above to get the area of the cross-section in terms of \(y\).
\[A\left( y \right) = \frac{{\sqrt 3 }}{4}{\left( {\frac{L}{h}y} \right)^2} = \frac{{\sqrt 3 {L^2}}}{{4{h^2}}}{y^2}\]Finally, we need the volume itself. We know that the volume is found by evaluating the following integral.
\[V = \int_{c}^{d}{{A\left( y \right)\,dy}}\]We already have a formula for \(A\left( y \right)\) from Step 2 and from the sketches in Step 1 we can see that the “first” cross-section will occur at \(y = 0\) and that the “last” cross-section will occur at \(y = h\) and so these are the limits for the integral.
The volume is then,
\[V = \int_{0}^{h}{{\frac{{\sqrt 3 {L^2}}}{{4{h^2}}}{y^2}\,dy}} = \frac{{\sqrt 3 {L^2}}}{{4{h^2}}}\int_{0}^{h}{{{y^2}\,dy}} = \left. {\frac{{\sqrt 3 {L^2}}}{{4{h^2}}}\left( {\frac{1}{3}{y^3}} \right)} \right|_0^h = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{\sqrt 3 \,{L^2}h}}{{12}}}}\]Do not get excited about the \(h\) and \(L\) in the integral and area formula. These are just constants. The only letter that is actually changing is \(y\). Because the \(h\) and \(L\) are constants we can factor them out of the integral as we did with the actual numbers.