Calculus I - More Volume Problems

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 6.5 : More Volume Problems

Back to Problem List

2. Find the volume of the solid whose base is a disk of radius $r$ and whose cross-sections are squares. See figure below to see a sketch of the cross-sections.

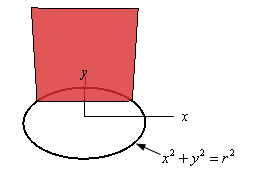
Show All Steps Hide All Steps

Start Solution

Here are a couple of sketches of the solid from three different angles. For reference the positive $x$ -axis and positive $y$ -axis are shown.

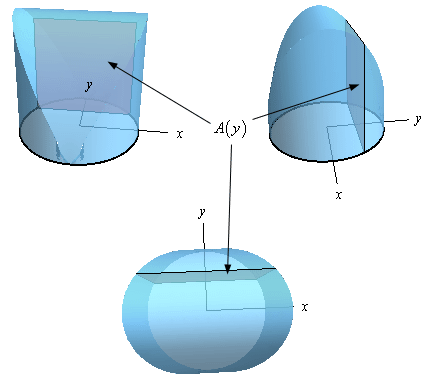
Because the cross-section is perpendicular to the $y$ -axis as we move the cross-section along the $y$ -axis we’ll change its area and so the cross-sectional area will be a function of $y$ , i.e. $A\left( y \right)$ .

Show Step 2

While the sketches above are nice to get a feel for what the solid looks like, what we really need is just a sketch of the cross-section. So, here’s a couple of sketches of the cross-sectional area.

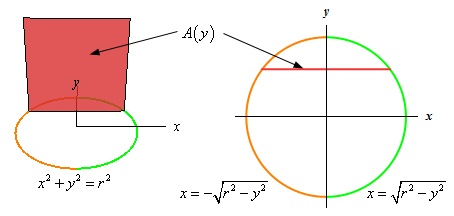
The sketch on the left is really just the graph given in the problem statement with the only difference that we colored the right/left sides so it will match with the sketch on the right. The sketch on the right looks at the cross-section from directly above and is shown by the red line.

Let’s get a quick sketch of just the cross-section and let’s call the length of the side of each square $s$ .

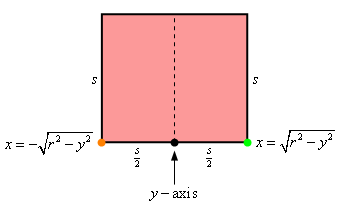
Now, along the bottom we’ve denoted the $y$ -axis location in the cross-section with a black dot and the orange and green dots represent where the left and right portions of the circle are at. We can also see that, assuming the cross-section is placed at some $y$ , the green dot must be a distance of $\sqrt {{r^2} - {y^2}}$ from the $y$ -axis. Likewise, the orange dot must also be a distance of $\sqrt {{r^2} - {y^2}}$ from the $y$ -axis (recall we want the distance to be positive here and so we drop the minus sign from the function to get a positive distance).

Now, we know that the area of the square is simply ${s^2}$ and from the discussion above we see that,

$\frac{s}{2} = \sqrt {{r^2} - {y^2}} \hspace{0.5in} \Rightarrow \hspace{0.5in}s = 2\sqrt {{r^2} - {y^2}}$

So, a formula for the area of the cross-section in terms of $y$ is,

$A\left( y \right) = {s^2} = {\left( {2\sqrt {{r^2} - {y^2}} } \right)^2} = 4\left( {{r^2} - {y^2}} \right)$ Show Step 3

Finally, we need the volume itself. We know that the volume is found by evaluating the following integral.

$V = \int_{c}^{d}{{A\left( y \right)\,dy}}$

We already have a formula for $A\left( y \right)$ from Step 2 and from the sketches in Step 1 we can see that the “first” cross-section will occur at $y = - r$ and that the “last” cross-section will occur at $y = r$ and so these are the limits for the integral.

The volume is then,

$V = \int_{{ - r}}^{r}{{4\left( {{r^2} - {y^2}} \right)\,dy}} = \left. {4\left( {y{r^2} - \frac{1}{3}{y^3}} \right)} \right|_{ - r}^r = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{16}}{3}{r^3}}}$

Do not get excited about the $r$ integral and area formula. It is just a constant. The only letter that is actually changing is $y$ .