Section 6.5 : More Volume Problems
3. Find the volume of the solid whose base is the region bounded by \(x = 2 - {y^2}\) and \(x = {y^2} - 2\) and whose cross-sections are isosceles triangles with the base perpendicular to the \(y\)-axis and the angle between the base and the two sides of equal length is \(\frac{\pi }{4}\). See figure below to see a sketch of the cross-sections.
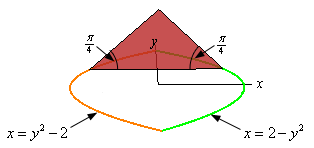
Show All Steps Hide All Steps
Here are a couple of sketches of the solid from three different angles. For reference the positive \(x\)-axis and positive \(y\)-axis are shown.
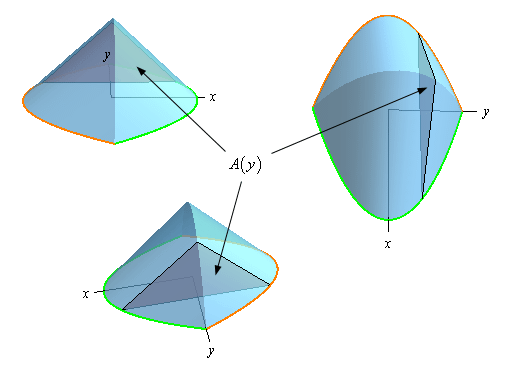
Because the cross-section is perpendicular to the \(y\)-axis as we move the cross-section along the \(y\)-axis we’ll change its area and so the cross-sectional area will be a function of \(y\), i.e. \(A\left( y \right)\).
While the sketches above are nice to get a feel for what the solid looks like, what we really need is just a sketch of the cross-section. So, here’s a couple of sketches of the cross-sectional area.
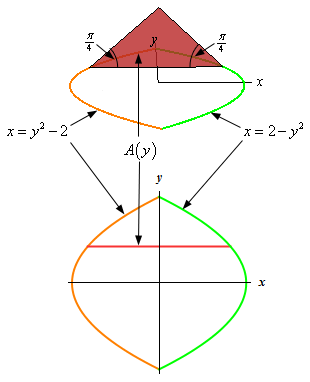
The sketch on the top is really just the graph given in the problem statement that is included for a reference with the sketch on the bottom. The sketch on the bottom looks at the cross-section from directly above and is shown by the red line.
Let’s get a quick sketch of just the cross-section and let’s call the length of the base of triangle \(b\) and the height of the triangle \(h\).
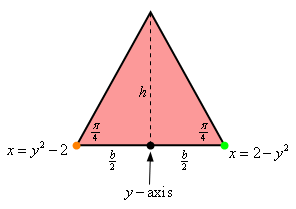
Now, along the bottom we’ve denoted the \(y\)-axis location in the cross-section with a black dot and the orange and green dots represent the left and right curves that define the left and right sides of the bottom of the solid. We can also see that, assuming the cross‑section is placed at some \(y\), the green dot must be a distance of \(2 - {y^2}\) from the \(y\)-axis. Likewise, the orange dot must also be a distance of \( - \left( {{y^2} - 2} \right) = 2 - {y^2}\) from the \(y\)-axis (recall we want the distance to be positive here and so we add the minus sign to the function to get a positive distance).
Now, we can see that the base of the triangle is given by,
\[\frac{b}{2} = 2 - {y^2}\hspace{0.5in} \Rightarrow \hspace{0.5in}b = 2\left( {2 - {y^2}} \right)\]Likewise, the height can be found from basic right triangle trig.
\[\tan \left( {\frac{\pi }{4}} \right) = \frac{h}{{{}^{b}/{}_{2}}}\hspace{0.5in} \Rightarrow \hspace{0.5in}h = \frac{b}{2}\tan \left( {\frac{\pi }{4}} \right) = 2 - {y^2}\]So, a formula for the area of the cross-section in terms of \(y\) is then,
\[A\left( y \right) = \frac{1}{2}bh = {\left( {2 - {y^2}} \right)^2} = 4 - 4{y^2} + {y^4}\]Finally, we need the volume itself. We know that the volume is found by evaluating the following integral.
\[V = \int_{c}^{d}{{A\left( y \right)\,dy}}\]By setting \(x = 0\) into either of the equations defining the left and right sides of the base of the solid (since they intersect at the \(y\)-axis) we can see that the “first” cross-section will occur at \(y = - \sqrt 2 \) and the “last” cross-section will occur at \(y = \sqrt 2 \) and so these are the limits for the integral.
The volume is then,
\[V = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{4 - 4{y^2} + {y^4}\,dy}} = \left. {\left( {4y - \frac{4}{3}{y^3} + \frac{1}{5}{y^5}} \right)} \right|_{ - \sqrt 2 }^{\sqrt 2 } = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{64\sqrt 2 }}{{15}}}}\]