Section 4.5 : The Shape of a Graph, Part I
6. For \(h\left( t \right) = 50 + 40{t^3} - 5{t^4} - 4{t^5}\) answer each of the following questions.
- Identify the critical points of the function.
- Determine the intervals on which the function increases and decreases.
- Classify the critical points as relative maximums, relative minimums or neither.
Show All Solutions Hide All Solutions
a Identify the critical points of the function. Show SolutionWe need the 1st derivative to get the critical points so here it is.
\[h'\left( t \right) = 120{t^2} - 20{t^3} - 20{t^4} = - 20{t^2}\left( {{t^2} + t - 6} \right) = - 20{t^2}\left( {t + 3} \right)\left( {t - 2} \right)\]Now, recall that critical points are where the derivative doesn’t exist or is zero. Clearly this derivative exists everywhere (it’s a polynomial….) and because we factored the derivative we can easily identify where the derivative is zero. The critical points of the function are,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{t = - 3,\,\,\,\,\,\,\,\,t = 0,\,\,\,\,\,\,\,t = 2}}\]b Determine the intervals on which the function increases and decreases. Show Solution
To determine the increase/decrease information for the function all we need is a quick number line for the derivative. Here is the number line.
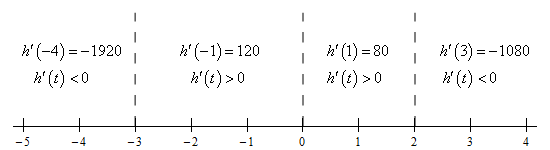
From this we get the following increasing/decreasing information for the function.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{{\mbox{Increasing : }}\left( { - 3,0} \right)\,\,\,\,\& \,\,\,\left( {0,2} \right)\hspace{0.25in}\hspace{0.25in}{\mbox{Decreasing : }}\,\,\left( { - \infty , - 3} \right)\,\,\,\,\& \,\,\,\,\left( {2,\infty } \right)}}\]c Classify the critical points as relative maximums, relative minimums or neither. Show Solution
With the increasing/decreasing information from the previous step we can easily classify the critical points using the 1st derivative test. Here is classification of the functions critical points.
\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{align*}t & = - 3 : {\mbox{ Relative Minimum}}\\ t & = 0 : {\mbox{Neither}}\\ t & = 2 : {\mbox{ Relative Maximum}}\end{align*}}\]