Section 2.1 : Tangent Lines And Rates Of Change
1. For the function \(f\left( x \right) = 3{\left( {x + 2} \right)^2}\) and the point \(P\) given by \(x = - 3\) answer each of the following questions.
- For the points \(Q\) given by the following values of \(x\) compute (accurate to at least 8 decimal places) the slope, \({m_{PQ}}\), of the secant line through points \(P\) and \(Q\).
- -3.5
- -3.1
- -3.01
- -3.001
- -3.0001
- -2.5
- -2.9
- -2.99
- -2.999
- -2.9999
- Use the information from (a) to estimate the slope of the tangent line to \(f\left( x \right)\) at \(x = - 3\) and write down the equation of the tangent line.
Show All Solutions Hide All Solutions
a For the points \(Q\) given by the following values of \(x\) compute (accurate to at least 8 decimal places) the slope, \({m_{PQ}}\), of the secant line through points \(P\) and \(Q\). Show Solution- -3.5
- -3.1
- -3.01
- -3.001
- -3.0001
- -2.5
- -2.9
- -2.99
- -2.999
- -2.9999
The first thing that we need to do is set up the formula for the slope of the secant lines. As discussed in this section this is given by,
\[{m_{PQ}} = \frac{{f\left( x \right) - f\left( { - 3} \right)}}{{x - \left( { - 3} \right)}} = \frac{{3{{\left( {x + 2} \right)}^2} - 3}}{{x + 3}}\]Now, all we need to do is construct a table of the value of \({m_{PQ}}\) for the given values of \(x\). All of the values in the table below are accurate to 8 decimal places, but in this case the values terminated prior to 8 decimal places and so the “trailing” zeros are not shown.
| \(x\) | \({m_{PQ}}\) | \(x\) | \({m_{PQ}}\) |
|---|---|---|---|
| -3.5 | -7.5 | -2.5 | -4.5 |
| -3.1 | -6.3 | -2.9 | -5.7 |
| -3.01 | -6.03 | -2.99 | -5.97 |
| -3.001 | -6.003 | -2.999 | -5.997 |
| -3.0001 | -6.0003 | -2.9999 | -5.9997 |
b Use the information from (a) to estimate the slope of the tangent line to \(f\left( x \right)\) at \(x = - 3\) and write down the equation of the tangent line. Show Solution
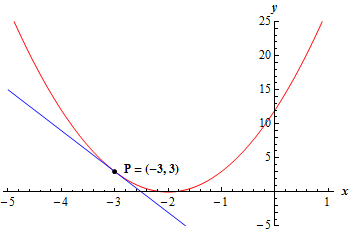
From the table of values above we can see that the slope of the secant lines appears to be moving towards a value of -6 from both sides of \(x = - 3\) and so we can estimate that the slope of the tangent line is : \(\require{bbox} \bbox[2pt,border:1px solid black]{{m = - 6}}\).
The equation of the tangent line is then,
\[y = f\left( { - 3} \right) + m\left( {x - \left( { - 3} \right)} \right) = 3 - 6\left( {x + 3} \right)\hspace{0.5in} \Rightarrow \hspace{0.5in}\,\require{bbox} \bbox[2pt,border:1px solid black]{{y = - 6x - 15}}\]Here is a graph of the function and the tangent line.