Section 2.2 : The Limit
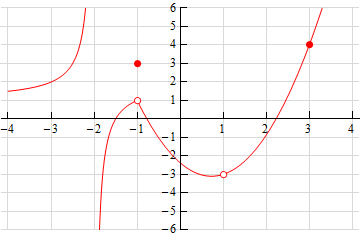
6. Below is the graph of \(f\left( x \right)\). For each of the given points determine the value of \(f\left( a \right)\) and \(\mathop {\lim }\limits_{x \to a} f\left( x \right)\). If any of the quantities do not exist clearly explain why.
- \(a = - 2\)
- \(a = - 1\)
- \(a = 1\)
- \(a = 3\)
Show All Solutions Hide All Solutions
a \(a = - 2\) Show SolutionBecause there is no closed dot for \(x = - 2\) we can see that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( { - 2} \right)\,\,\,{\mbox{does not exist}}}}\]We can also see that as we approach \(x = - 2\) from both sides the graph is not approaching a value from either side and so we get,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to - 2} f\left( x \right)\,\,\,{\mbox{does not exist}}}}\]b \(a = - 1\) Show Solution
From the graph we can see that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( { - 1} \right) = 3}}\]because the closed dot is at the value of \(y = 3\).
We can also see that as we approach \(x = - 1\) from both sides the graph is approaching the same value, 1, and so we get,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = 1}}\]Always recall that the value of a limit does not actually depend upon the value of the function at the point in question. The value of a limit only depends on the values of the function around the point in question. Often the two will be different.
c \(a = 1\) Show Solution
Because there is no closed dot for \(x = 1\) we can see that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( 1 \right)\,\,\,{\mbox{does not exist}}}}\]We can also see that as we approach \(x = 1\) from both sides the graph is approaching the same value, -3, and so we get,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to 1} f\left( x \right) = - 3}}\]Always recall that the value of a limit does not actually depend upon the value of the function at the point in question. The value of a limit only depends on the values of the function around the point in question. Therefore, even though the function doesn’t exist at this point the limit can still have a value.
d \(a = 3\) Show Solution
From the graph we can see that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{f\left( 3 \right) = 4}}\]because the closed dot is at the value of \(y = 4\).
We can also see that as we approach \(x = 3\) from both sides the graph is approaching the same value, 4, and so we get,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{x \to 3} f\left( x \right) = 4}}\]