Section 1.4 : Solving Trig Equations
3. Without using a calculator find all the solutions to \(\displaystyle 2\cos \left( {\frac{x}{3}} \right) + \sqrt 2 = 0\).
Show All Steps Hide All Steps
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
\[\cos \left( {\frac{x}{3}} \right) = - \frac{{\sqrt 2 }}{2}\]Because we’re dealing with cosine in this problem and we know that the \(x\)-axis represents cosine on a unit circle we’re looking for angles that will have a \(x\) coordinate of \( - \frac{{\sqrt 2 }}{2}\). This means that we’ll have angles in the second and third quadrant.
Because of the negative value we can’t just find the corresponding angle in the first quadrant and use that to find the second angle. However, we can still use the angles in the first quadrant to find the two angles that we need. Here is a unit circle for this situation.
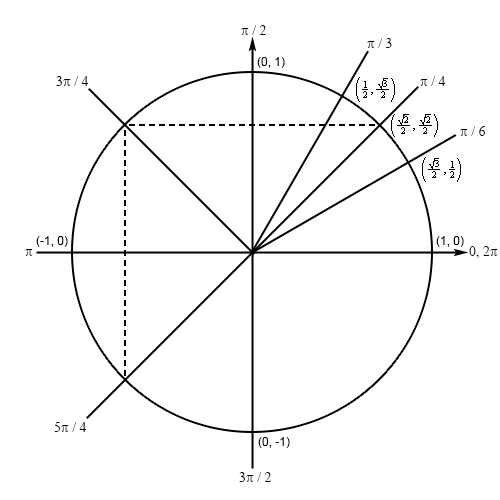
If we didn’t have the negative value then the angle would be \(\frac{\pi }{4}\). Now, based on the symmetry in the unit circle, the terminal line for both of the angles will form an angle of \(\frac{\pi }{4}\) with the negative \(x\)-axis. The angle in the second quadrant will then be \(\pi - \frac{\pi }{4} = \frac{{3\pi }}{4}\) and the angle in the third quadrant will be \(\pi + \frac{\pi }{4} = \frac{{5\pi }}{4}\).
From the discussion in the notes for this section we know that once we have these two angles we can get all possible angles by simply adding “\( + \,2\pi n\) for \(n = 0, \pm 1, \pm 2, \ldots \)” onto each of these.
This then means that we must have,
\[\frac{x}{3} = \frac{{3\pi }}{4} + 2\pi n \hspace{0.5in} {\rm{OR }} \hspace{0.5in} \frac{x}{3} = \frac{{5\pi }}{4} + 2\pi n \hspace{0.5in} n = 0, \pm 1, \pm 2, \ldots \]Finally, to get all the solutions to the equation all we need to do is multiply both sides by 3.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{x = \frac{{9\pi }}{4} + 6\pi n \hspace{0.5in} {\rm{OR }} \hspace{0.5in} x = \frac{{15\pi }}{4} + 6\pi n \hspace{0.5in} n = 0, \pm 1, \pm 2, \ldots }}\]