Section 1.5 : Solving Trig Equations with Calculators, Part I
4. Find the solution(s) to \(\displaystyle 4\sin \left( {6z} \right) + \frac{{13}}{{10}} = - \frac{3}{{10}}\) that are in \(\left[ {0,2} \right]\). Use at least 4 decimal places in your work.
Show All Steps Hide All Steps
Isolating the sine (with a coefficient of one) on one side of the equation gives,
\[\sin \left( {6z} \right) = - \frac{2}{5}\]First, using our calculator we can see that,
\[6z = {\sin ^{ - 1}}\left( { - \frac{2}{5}} \right) = - 0.4115\]Now we’re dealing with sine in this problem and we know that the \(y\)-axis represents sine on a unit circle and so we’re looking for angles that will have a \(y\) coordinate of \( - \frac{2}{5}\). This means that we’ll have angles in the fourth (this is the one our calculator gave us) and third quadrant. Here is a unit circle for this situation.
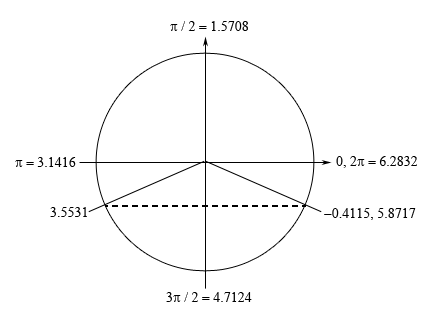
From the symmetry of the unit circle we can see that the second angle will make an angle of 0.4115 with the negative \(x\)-axis and so the second angle will be \(\pi + 0.4115 = 3.5531\). Also, as noted on the unit circle above a positive angle that represents the first angle (i.e. the angle in the fourth quadrant) is \(2\pi - 0.4115 = 5.8717\). We can use either the positive or the negative angle here and we’ll get the same solutions. However, because it is often easy to lose track of minus signs we will be using the positive angle in the fourth quadrant for our work here.
From the discussion in the notes for this section we know that once we have these two angles we can get all possible angles by simply adding “\( + \,2\pi n\) for \(n = 0, \pm 1, \pm 2, \ldots \)” onto each of these.
This then means that we must have,
\[6z = 3.5531 + 2\pi n\hspace{0.25in}{\mbox{OR }}\hspace{0.25in}6z = 5.8717 + 2\pi n\hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \]Finally, to get all the solutions to the equation all we need to do is divide both sides by 6 and we’ll convert everything to decimals to help with the final step.
\[\begin{align*}z & = 0.5922 + \frac{{\pi n}}{3} & \hspace{0.25in}{\mbox{OR }}\hspace{0.25in} & z = 0.9786 + \frac{{\pi n}}{3}\hspace{0.25in} & n = 0, \pm 1, \pm 2, \ldots \\ & = 0.5922 + 1.0472n & \hspace{0.25in}{\mbox{OR }}\hspace{0.25in} &\hspace{0.10in} = 0.9786 + 1.0472n\hspace{0.25in} & n = 0, \pm 1, \pm 2, \ldots \end{align*}\]Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of \(n\) we will get negative solutions and these will not be in the interval and so there is no reason to even try these. So, let’s start at \(n = 0\) and see what we get.
\[\begin{array}{lclcl}{n = 0:\,} & {z = 0.5922\,} & \hspace{0.25in} {{\mbox{OR}}} \hspace{0.25in} & {z = 0.9786}\\{n = 1:} & {z = 1.6394\,} & \hspace{0.25in} {{\mbox{OR}}} \hspace{0.25in} & {\require{cancel} \hspace{0.35in} \xcancel{{z = 2.0258}} > 2}\end{array}\]Notice that with each increase in \(n\) we were really just adding another 1.0472 onto the previous results and by doing this to the results from the \(n = 1\) step we will get solutions that are outside of the interval and so there is no reason to even plug in \(n = 2\). Also, as we’ve seen in this problem it is completely possible for only one of the solutions from a given interval to be in the given interval so don’t worry about that when it happens.
So, it looks like we have the three solutions to this equation in the given interval.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{z = 0.5922,\,\,0.9786,\,\,1.6394}}\]Note that depending upon the amount of decimals you used here your answers may vary slightly from these due to round off error. Any differences should be slight and only appear around the 4th decimal place or so however.