Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 1.3 : Trig Functions
10. Determine the exact value of \(\displaystyle \sin \left( { - \frac{{11\pi }}{3}} \right)\) without using a calculator.
Show All Steps Hide All Steps
Hint : Sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
First we can notice that \(\frac{\pi }{3} - 4\pi = - \frac{{11\pi }}{3}\) and note that \(4\pi \) is two complete revolutions (also, remembering that negative angles are rotated clockwise) we can see that the terminal line for \( - \frac{{11\pi }}{3}\) and \(\frac{\pi }{3}\) are the same angle and so we’ll have the following unit circle for this problem.
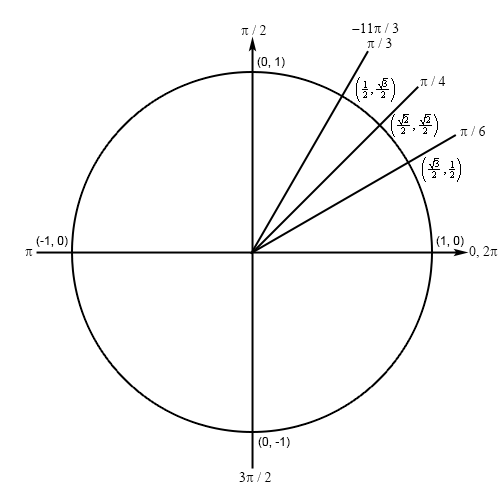
Hint : Given the very obvious symmetry here write down the answer to the question.
Because \( - \frac{{11\pi }}{3}\) and \(\frac{\pi }{3}\) are the same angle the answer is,
\[\sin \left( { - \frac{{11\pi }}{3}} \right) = \frac{{\sqrt 3 }}{2}\]