Section 9.8 : Area with Polar Coordinates
2. Find the area inside the graph of \(r = 7 + 3\cos \theta \) and to the left of the \(y\)-axis.
Show All Steps Hide All Steps
Start SolutionFirst, here is a quick sketch of the graph of the region we are interested in.
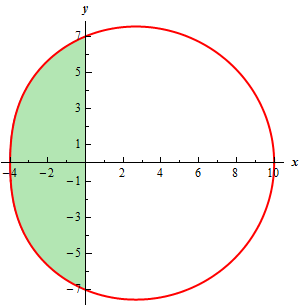
For this problem there isn’t too much difficulty in getting the limits for the problem. We will need to use the limits \(\frac{\pi }{2} \le \theta \le \frac{{3\pi }}{2}\) to trace out the portion of the graph to the left of the \(y\)-axis.
Remember that it is important to trace out the portion of the curve defining the area we are interested in as the \(\theta \)’s increase from the smaller to larger value.
Show Step 3The area is then,
\[\begin{align*}A & = \int_{{\frac{\pi }{2}}}^{{\frac{{3\pi }}{2}}}{{\frac{1}{2}{{\left( {7 + 3\cos \theta } \right)}^2}\,d\theta }}\\ & = \frac{1}{2}\int_{{\frac{\pi }{2}}}^{{\frac{{3\pi }}{2}}}{{49 + 42\cos \theta + 9co{s^2}\left( \theta \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{\frac{\pi }{2}}}^{{\frac{{3\pi }}{2}}}{{49 + 42\cos \theta + \frac{9}{2}\left( {1 + \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{\frac{\pi }{2}}}^{{\frac{{3\pi }}{2}}}{{\frac{{107}}{2} + 42\cos \theta + \frac{9}{2}\cos \left( {2\theta } \right)\,d\theta }}\\ & = \left. {\frac{1}{2}\left( {\frac{{107}}{2}\theta + 42\sin \left( \theta \right) + \frac{9}{4}\sin \left( {2\theta } \right)} \right)} \right|_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} = \require{bbox} \bbox[2pt,border:1px solid black]{{42.0376}}\end{align*}\]Make sure you can do the trig manipulations required to do these integrals. Most of the integrals in this section will involve this kind of manipulation. If you don’t recall how to do them go back and take a look at the Integrals Involving Trig Functions section.