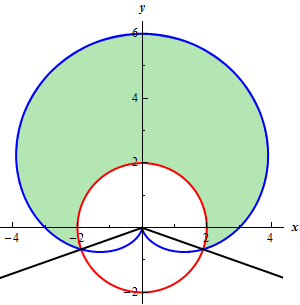
Now, we’ll need to determine the values of \(\theta \) where the graphs intersect (indicated by the black lines on the graph in the previous step).

There are easy enough to find. Because they are where the graphs intersect we know they must have the same value of \(r\). So,

\[\begin{align*}3 + 3\sin \theta & = 2\\ \sin \theta & = - \frac{1}{3}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = {\sin ^{ - 1}}\left( { - \frac{1}{3}} \right) = - 0.3398\end{align*}\]

This is the angle in the fourth quadrant where the graphs intersect.

From a quick sketch of a unit circle we can quickly get the angle in the third quadrant where the two graphs intersect.

\[\theta = \pi + 0.3398 = 3.4814\]

The ranges of \(\theta \) for this problem is then \( - 0.3398 \le \theta \le 3.4814\).

Show Step 3

From the graph we can see that \(r = 3 + 3\sin \theta \) is the “outer” graph for this region and \(r = 2\) is the “inner” graph.

The area is then,

\[\begin{align*}A & = \int_{{ - 0.3398}}^{{3.4814}}{{\frac{1}{2}\left[ {{{\left( {3 + 3\sin \theta } \right)}^2} - {{\left( 2 \right)}^2}} \right]\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 0.3398}}^{{3.4814}}{{5 + 18\sin \theta + 9{{\sin }^2}\left( \theta \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 0.3398}}^{{3.4814}}{{5 + 18\sin \theta + \frac{9}{2}\left( {1 - \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 0.3398}}^{{3.4814}}{{\frac{{19}}{2} + 18\sin \theta - \frac{9}{2}\cos \left( {2\theta } \right)\,d\theta }}\\ & = \left. {\frac{1}{2}\left( {\frac{{19}}{2}\theta - 18\cos \left( \theta \right) - \frac{9}{4}\sin \left( {2\theta } \right)} \right)} \right|_{ - 0.3398}^{3.4814} = \require{bbox} \bbox[2pt,border:1px solid black]{{33.7074}}\end{align*}\]

Make sure you can do the trig manipulations required to do these integrals. Most of the integrals in this section will involve this kind of manipulation. If you don’t recall how to do them go back and take a look at the Integrals Involving Trig Functions section.