Section 9.6 : Polar Coordinates
1. For the point with polar coordinates \(\displaystyle \left( {2,\frac{\pi }{7}} \right)\) determine three different sets of coordinates for the same point all of which have angles different from \(\displaystyle \frac{\pi }{7}\) and are in the range \( - 2\pi \le \theta \le 2\pi \).
Show All Steps Hide All Steps
Start SolutionThis problem is really as exercise in how well we understand the unit circle. Here is a quick sketch of the point and some angles.
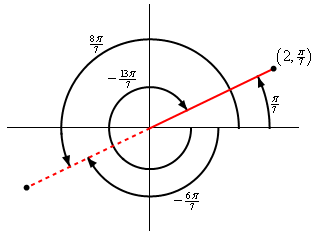
We can see that the negative angle ending at the solid red line that is in the range specified in the problem statement is simply \(\frac{\pi }{7} - 2\pi = - \frac{{13\pi }}{7}\).
If we extend the solid line into the third quadrant (i.e. the dashed red line) then the positive angle ending at the dashed red line is \(\frac{\pi }{7} + \pi = \frac{{8\pi }}{7}\). Likewise, the negative angle ending at the dashed red line is \(\frac{\pi }{7} - \pi = - \frac{{6\pi }}{7}\).
With these angles getting the other three points should be pretty simple.
Show Step 2For the first “new” point we can use the negative angle that ends on the solid red line to get the point.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\left( {2, - \frac{{13\pi }}{7}} \right)}}\] Show Step 3For the remaining points recall that if we use a negative \(r\) then we go “backwards” from where the angle ends to get the point. So, if we use \(r = - 2\), any angle that ends on the dashed red line will go “backwards” into the first quadrant 2 units to get to the point.
This gives the remaining two points using both the positive and negative angle ending on the dashed red line,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\left( { - 2, - \frac{{6\pi }}{7}} \right)}}\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\require{bbox} \bbox[2pt,border:1px solid black]{{\left( { - 2,\frac{{8\pi }}{7}} \right)}}\]