Section 15.8 : Change of Variables
9. Evaluate \(\displaystyle \iint\limits_{R}{{x + 2y\,dA}}\) where \(R\) is the triangle with vertices \(\left( {0,3} \right)\), \(\left( {4,1} \right)\) and \(\left( {2,6} \right)\) using the transformation \(\displaystyle x = \frac{1}{2}\left( {u - v} \right)\), \(\displaystyle y = \frac{1}{4}\left( {3u + v + 12} \right)\) to \(R\).
Show All Steps Hide All Steps
Start SolutionThe first thing we need to do is determine the transformation of \(R\).
First, a sketch of \(R\).
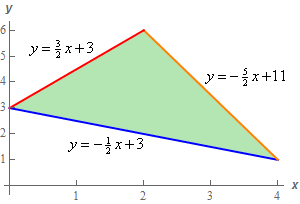
The equations of each of the boundaries of the region are given in the sketch. Given that we know the coordinates of each of the vertices its simple algebra to determine the equation of a line given two points on the line so we’ll leave it to you to verify the equations.
Note that integrating over this region would require two integrals regardless of the order. You can see how each order of integration would require two integrals correct?
Now, let’s transform each of the boundary curves.
\(\displaystyle y = \frac{3}{2}x + 3:\hspace{0.25in}\,\,\,\,\frac{1}{4}\left( {3u + v + 12} \right) = \frac{3}{2}\left( {\frac{1}{2}} \right)\left( {u - v} \right) + 3\,\,\,\,\hspace{0.25in}\to \,\,\,\,\,\,\,v = 0\)\(\displaystyle y = - \frac{5}{2}x + 11:\hspace{0.25in}\frac{1}{4}\left( {3u + v + 12} \right) = - \frac{5}{2}\left( {\frac{1}{2}} \right)\left( {u - v} \right) + 11\,\,\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,v = 2u - 8\)
\(\displaystyle y = - \frac{1}{2}x + 3:\hspace{0.25in}\frac{1}{4}\left( {3u + v + 12} \right) = - \frac{1}{2}\left( {\frac{1}{2}} \right)\left( {u - v} \right) + 3\,\hspace{0.25in}\to \,\,\,\,\,\,\,u = 0\)
Note that, in this case, the first and last boundary equation we looked at above just ended up being transformed into the \(u\)-axis and \(v\)-axis respectively. That will happen on occasion and might well end up making our life a little easier when it comes to evaluating the integral.
Here is a sketch of the transformed region and note that the transformed region will be much easier to integrate over than the original region.
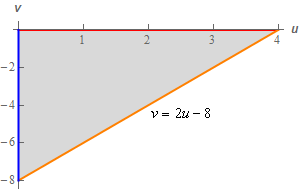
So, the limits for the transformed region are,
\[\begin{array}{c}0 \le u \le 4\\ 2u - 8 \le v \le 0\end{array}\]Note as well that this is going to be a much nice region to integrate over than the original region.
Show Step 2We’ll need the Jacobian of this transformation next.
\[\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}} = \left| {\begin{array}{*{20}{c}}{\displaystyle \frac{{\partial x}}{{\partial u}}}&\displaystyle {\frac{{\partial x}}{{\partial v}}}\\\displaystyle {\frac{{\partial y}}{{\partial u}}}&\displaystyle {\frac{{\partial y}}{{\partial v}}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}}{\displaystyle \frac{1}{2}}&{\displaystyle - \frac{1}{2}}\\{\displaystyle \frac{3}{4}}&{\displaystyle \frac{1}{4}}\end{array}} \right| = \frac{1}{8} - \left( { - \frac{3}{8}} \right) = \frac{1}{2}\] Show Step 3We can now write the integral in terms of the “new” \(uv\) coordinates system.
\[\begin{align*}\iint\limits_{R}{{x + 2y\,dA}} & = \int_{0}^{4}{{\int_{{2u - 8}}^{0}{{\left[ {\frac{1}{2}\left( {u - v} \right) + 2\left( {\frac{1}{4}} \right)\left( {3u + v + 12} \right)} \right]\left| {\frac{1}{2}} \right|\,dv}}\,du}}\\ & = \int_{0}^{4}{{\int_{{2u - 8}}^{0}{{u + 3\,dv}}\,du}}\end{align*}\]Don’t forget to add in the Jacobian and don’t forget that the absolute value bars on it. In this case we can just drop the absolute value bars since we just have a positive number in the absolute value.
Also, the simplified integrand didn’t suggest any one order of integration over the other and so we just chose one to work with. The other order would be just as easy to have worked with.
Show Step 4Finally, let’s evaluate the integral.
\[\begin{align*}\iint\limits_{R}{{x + 2y\,dA}} & = \int_{0}^{4}{{\int_{{2u - 8}}^{0}{{u + 3\,dv}}\,du}}\\ & = \int_{0}^{4}{{\left. {\left( {u + 3} \right)v} \right|_{2u - 8}^0\,du}}\\ & = \int_{0}^{4}{{\left( {u + 3} \right)\left( { - 2u + 8} \right)\,du}}\\ & = \int_{0}^{4}{{24 + 2u - 2{u^2}\,du}}\\ & = \left. {\left( {24u + {u^2} - \frac{2}{3}{u^3}} \right)} \right|_0^4\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{208}}{3}}}\end{align*}\]