Calculus III - Parametric Surfaces

Show Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 17.2 : Parametric Surfaces

Back to Problem List

9. Determine the surface area of the portion of $z = 3 + 2y + \frac{1}{4}{x^4}$ that is above the region in the $xy$ -plane bounded by $y = {x^5}$ , $x = 1$ and the $x$ -axis.

Show All Steps Hide All Steps

Start Solution

Parameterizing this surface is pretty simple. We have the equation of the surface in the form $z = f\left( {x,y} \right)$ and so the parameterization of the surface is,

$\vec r\left( {x,y} \right) = \left\langle {x,y,3 + 2y + \frac{1}{4}{x^4}} \right\rangle$

Now, this is the parameterization of the full surface and we only want the portion that lies over the following region.

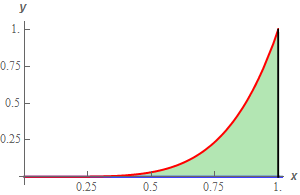
So, to get only the portion of the surface we’ll need to restrict $x$ and $y$ to the following ranges,

$\begin{align*}0 \le x \le 1\\ & 0 \le y \le {x^5}\end{align*}$

On a side note we can see that we are in the 1^st quadrant here and so we know that $x \ge 0$ and $y \ge 0$ . Therefore, we can see that the surface in the 1^st quadrant is always above the $xy$ -plane and so will in fact always be above the region above as suggested in the problem statement.

Show Step 2

Next, we need to compute ${\vec r_x} \times {\vec r_y}$ . Here is that work.

${\vec r_x} = \left\langle {1,0,{x^3}} \right\rangle \hspace{0.5in}{\vec r_y} = \left\langle {0,1,2} \right\rangle$

${\vec r_x} \times {\vec r_y} = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\1&0&{{x^3}}\\0&1&2\end{array}} \right| = - {x^3}\vec i - 2\vec j + \vec k$

Now, we what we really need is,

$\left\| {{{\vec r}_x} \times {{\vec r}_y}} \right\| = \sqrt {{{\left( { - {x^3}} \right)}^2} + {{\left( { - 2} \right)}^2} + {{\left( 1 \right)}^2}} = \sqrt {{x^6} + 5}$ Show Step 3

The integral for the surface area is then,

$A = \iint\limits_{D}{{\sqrt {{x^6} + 5} \,dA}} = \int_{0}^{1}{{\int_{0}^{{{x^5}}}{{\sqrt {{x^6} + 5} \,dy}}\,dx}}$

As noted in the integral above $D$ is just the ranges of $x$ and $y$ we found in Step 1.

Show Step 4

Now we just need to evaluate the integral to get the surface area.

$\begin{align*}A & = \int_{0}^{1}{{\int_{0}^{{{x^5}}}{{\sqrt {{x^6} + 5} \,dy}}\,dx}} = \int_{0}^{1}{{\left. {y\sqrt {{x^6} + 5} } \right|_0^{{x^5}}\,dx}}\\ & = \int_{0}^{1}{{{x^5}\,\sqrt {{x^6} + 5} \,dx}} = \left. {\frac{1}{9}{{\left( {{x^6} + 5} \right)}^{\frac{3}{2}}}} \right|_0^1 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{1}{9}\left( {{6^{\frac{3}{2}}} - {5^{\frac{3}{2}}}} \right) = 0.3907}}\end{align*}$