Show All Notes Hide All Notes

Section 3.2 : Interpretation of the Derivative

For problems 1 and 2 use the graph of the function, \(f\left( x \right)\), estimate the value of \(f'\left( a \right)\) for the given values of \(a\).

1. 1. \(a = - 2\)
   2. \(a = 3\)
   
   Solution
2. 1. \(a = 1\)
   2. \(a = 4\)
   
   Solution

For problems 3 and 4 sketch the graph of a function that satisfies the given conditions.

1. \(f\left( 1 \right) = 3\), \(f'\left( 1 \right) = 1\), \(f\left( 4 \right) = 5\), \(f'\left( 4 \right) = - 2\) Solution
2. \(f\left( { - 3} \right) = 5\), \(f'\left( { - 3} \right) = - 2\), \(f\left( 1 \right) = 2\), \(f'\left( 1 \right) = 0\), \(f\left( 4 \right) = - 2\), \(f'\left( 4 \right) = - 3\) Solution

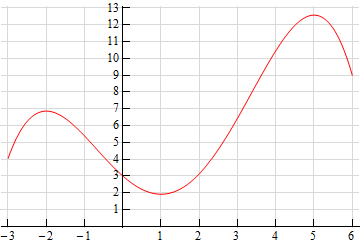
For problems 5 and 6 the graph of a function, \(f\left( x \right)\), is given. Use this to sketch the graph of the derivative, \(f'\left( x \right)\).

1. 
   Solution
2. 
   Solution
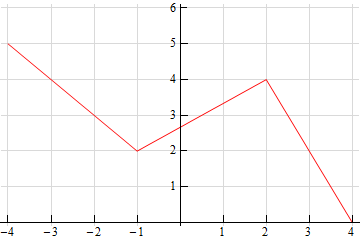
3. Answer the following questions about the function \(W\left( z \right) = 4{z^2} - 9z\).
   1. Is the function increasing or decreasing at \(z = - 1\)?
   2. Is the function increasing or decreasing at \(z = 2\)?
   3. Does the function ever stop changing? If yes, at what value(s) of \(z\) does the function stop changing?
   Solution
4. What is the equation of the tangent line to \(f\left( x \right) = 3 - 14x\) at \(x = 8\). Solution
5. The position of an object at any time \(t\) is given by \(\displaystyle s\left( t \right) = \frac{{t + 1}}{{t + 4}}\).
   1. Determine the velocity of the object at any time \(t\).
   2. Does the object ever stop moving? If yes, at what time(s) does the object stop moving?
   Solution
6. What is the equation of the tangent line to \(\displaystyle f\left( x \right) = \frac{5}{x}\) at \(\displaystyle x = \frac{1}{2}\)? Solution
7. Determine where, if anywhere, the function \(g\left( x \right) = {x^3} - 2{x^2} + x - 1\) stops changing. Solution
8. Determine if the function \(Z\left( t \right) = \sqrt {3t - 4} \) increasing or decreasing at the given points.
   1. \(t = 5\)
   2. \(t = 10\)
   3. \(t = 300\)
   Solution
9. Suppose that the volume of water in a tank for\(0 \le t \le 6\) is given by \(Q\left( t \right) = 10 + 5t - {t^2}\).
   1. Is the volume of water increasing or decreasing at \(t = 0\)?
   2. Is the volume of water increasing or decreasing at \(t = 6\)?
   3. Does the volume of water ever stop changing? If yes, at what times(s) does the volume stop changing?
   Solution