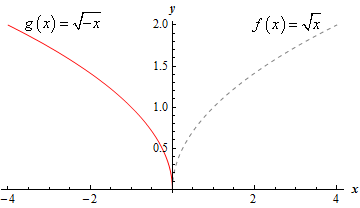Section 1.10 : Common Graphs
10. Without using a graphing calculator sketch the graph of \(g\left( x \right) = \sqrt { - x} \).
First, do not get excited about the minus sign under the root. We all know that we won’t get real numbers if we take the square root of a negative number, but that minus sign doesn’t necessarily mean that we’ll be taking the square root of negative numbers. If we plug in positive value of \(x\) then clearly we will be taking the square root of negative numbers, but if we plug in negative values of \(x\) we will now be taking the square root of positive numbers and so there really is nothing wrong with the function as written. We’ll just be using a different set of \(x\)’s than what we may be used to working with when dealing with square roots.
Now, recall the basic Algebraic transformations. If we know the graph of \(f\left( x \right)\) then the graph of \(f\left( { - x} \right)\) is simply the graph of \(f\left( x \right)\) reflected about the \(y\)-axis.
So, in our case if \(f\left( x \right) = \sqrt x \) we can see that,
\[g\left( x \right) = \sqrt { - x} = f\left( { - x} \right)\]and so the graph we’re being asked to sketch is the graph of the square root function reflected about the \(y\)-axis.
Here is the graph of \(g\left( x \right) = \sqrt { - x} \) and note that to help see the transformation we have also sketched in the graph of \(f\left( x \right) = \sqrt x \).