Section 1.10 : Common Graphs
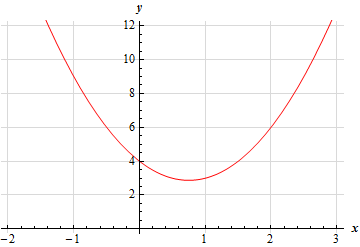
11. Without using a graphing calculator sketch the graph of \(h\left( x \right) = 2{x^2} - 3x + 4\).
We know that the graph of \(f\left( x \right) = a{x^2} + bx + c\) will be a parabola that opens upwards if \(a > 0\) and opens downwards if \(a < 0\). We also know that its vertex is at,
\[\left( { - \frac{b}{{2a}},f\left( { - \frac{b}{{2a}}} \right)} \right)\]The \(y\)-intercept of the parabola is the point \(\left( {0,f\left( 0 \right)} \right) = \left( {0,c} \right)\) and the \(x\)-intercepts (if any) are found by solving \(f\left( x \right) = 0\).
So, or our case we know we have a parabola that opens upwards and that its vertex is at,
\[\left( { - \frac{{ - 3}}{{2\left( 2 \right)}},f\left( { - \frac{{ - 3}}{{2\left( 2 \right)}}} \right)} \right) = \left( {\frac{3}{4},f\left( {\frac{3}{4}} \right)} \right) = \left( {\frac{3}{4},\frac{{23}}{8}} \right) = \left( {0.75,\,\,2.875} \right)\]We can also see that the \(y\)-intercept is \(\left( {0,4} \right)\). Because the vertex is above the \(x\)-axis and the parabola opens upwards we can see that there will be no \(x\)-intercepts.
It is usually best to have at least one point on either side of the vertex and we know that parabolas are symmetric about the vertical line running through the vertex. Therefore, because we know that the \(y\)-intercept is 0.75 units to the left of the vertex that we must also have a point that is 0.75 to the right of the vertex with the same \(y\)-value and this point is : \(\left( {1.5,4} \right)\).
Here is a sketch of this parabola.