We know that the graph of \(f\left( y \right) = a{y^2} + by + c\) will be a parabola that opens towards the right if \(a > 0\) and opens towards the left if \(a < 0\). We also know that its vertex is at,

\[\left( {f\left( { - \frac{b}{{2a}}} \right), - \frac{b}{{2a}}} \right)\]

The \(x\)-intercept of the parabola is the point \(\left( {f\left( 0 \right),0} \right) = \left( {c,0} \right)\) and the \(y\)-intercepts (if any) are found by solving \(f\left( y \right) = 0\)

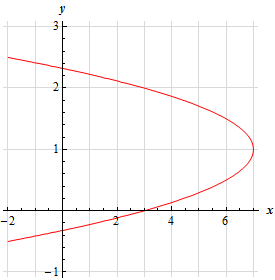
So, or our case we know we have a parabola that opens towards the left and that its vertex is at,

\[\left( {f\left( { - \frac{8}{{2\left( { - 4} \right)}}} \right), - \frac{8}{{2\left( { - 4} \right)}}} \right) = \left( {f\left( 1 \right),1} \right) = \left( {7,1} \right)\]

We can also see that the \(x\)-intercept is \(\left( {3,0} \right)\).

To find the \(y\)-intercepts all we need to do is solve : \( - 4{y^2} + 8y + 3 = 0\).

\[y = \frac{{ - 8 \pm \sqrt {{8^2} - 4\left( { - 4} \right)\left( 3 \right)} }}{{2\left( { - 4} \right)}} = \frac{{ - 8 \pm \sqrt {112} }}{{ - 8}} = \frac{{ - 8 \pm 4\sqrt 7 }}{{ - 8}} = \frac{{2 \pm \sqrt 7 }}{2} = - 0.3229,\,\,\,2.3229\]

So, the two \(y\)-intercepts are : \(\left( {0, - 0.3229} \right)\) and \(\left( {0,2.3229} \right)\).

Here is a sketch of this parabola.