Section 1.10 : Common Graphs
6. Without using a graphing calculator sketch the graph of \(h\left( x \right) = {\left( {x - 3} \right)^2} + 4\).
The Algebraic transformations we were using in the first few problems of this section can be combined to shift a graph up/down and right/left at the same time. If we know the graph of \(g\left( x \right)\) then the graph of \(g\left( {x + c} \right) + k\) is simply the graph of \(g\left( x \right)\) shifted right by \(c\) units if \(c < 0\) or shifted left by \(c\) units if \(c > 0\) and shifted up by \(k\) units if \(k > 0\) or shifted down by \(k\) units if \(k < 0\).
So, in our case if \(g\left( x \right) = {x^2}\) we can see that,
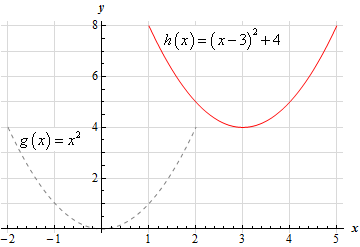
\[h\left( x \right) = {\left( {x - 3} \right)^2} + 4 = g\left( {x - 3} \right) + 4\]and so the graph we’re being asked to sketch is the graph of \(g\left( x \right) = {x^2}\)shifted right by 3 units and up by 4 units.
Here is the graph of \(h\left( x \right) = {\left( {x - 3} \right)^2} + 4\) and note that to help see the transformation we have also sketched in the graph of \(g\left( x \right) = {x^2}\).