Section 2.3 : One-Sided Limits
4. Sketch a graph of a function that satisfies each of the following conditions.
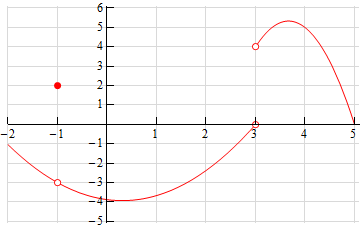
\[\begin{array}{ccl}\mathop {\lim }\limits_{x \to {3^{\, - }}} f\left( x \right) = 0 & \hspace{0.5in}\mathop {\lim }\limits_{x \to {3^{\, + }}} f\left( x \right) = 4 & \hspace{0.5in}f\left( 3 \right){\mbox{ does not exist}}\\ \mathop {\lim }\limits_{x \to - 1} f\left( x \right) = - 3 & \hspace{0.5in} f\left( { - 1} \right) = 2 & \end{array}\] Show SolutionThere are literally an infinite number of possible graphs that we could give here for an answer. However, all of them must the following two sets of criteria.
First, at \(x = 3\) there cannot be a closed dot on the graph (as indicated by the fact that the function does not exist here), the graph must be approaching a value of 0 as it approaches \(x = 3\) from the left (as indicated by the left-hand limit) and it must be approaching a value of 4 as it approaches \(x = 3\) from the right (as indicated by the right-hand limit).
Next, the graph must have a closed dot at the point \(\left( { - 1,2} \right)\) and the graph must be approaching a value of -3 as it approaches \(x = - 1\) from both sides (as indicated by the fact that value of the overall limit is -3 at this point).
Here is a sketch of one possible graph that meets these conditions.