Calculus I - Related Rates

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 3.11 : Related Rates

Back to Problem List

5. A person is standing 350 feet away from a model rocket that is fired straight up into the air at a rate of 15 ft/sec. At what rate is the distance between the person and the rocket increasing (a) 20 seconds after liftoff? (b) 1 minute after liftoff?

Show All Steps Hide All Steps

Start Solution

Here is a sketch for this situation that will work for both parts so we’ll put it here.

Show Step 2

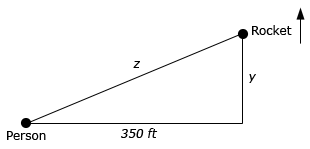
In both parts we know that \(y' = 15\) and want to determine \(z'\) for each given time. Using the Pythagorean Theorem we get the following equation to relate \(y\) and \(z\).

\[{z^2} = {y^2} + {350^2} = {y^2} + 122500\] Show Step 3

Finally, let’s differentiate this with respect to \(t\) and we can even solve it for \(z'\) so the actual solution will be quick and simple to find.

\[2z\,z' = 2y\,y'\hspace{0.5in} \Rightarrow \hspace{0.5in}z' = \frac{{y\,y'}}{z}\]

We have now reached a point where the process will differ for each part.

a At what rate is the distance between the person and the rocket increasing 20 seconds after liftoff? Show Solution

To finish off this problem all we need to do is determine \(y\) (from the speed of the rocket and given time) and \(z\) (reusing the Pythagorean Theorem).

\[y = \left( {15} \right)\left( {20} \right) = 300\hspace{0.5in}z = \sqrt {{{300}^2} + {{350}^2}} = \sqrt {212500} = 50\sqrt {85} = 460.9772\]

The rate of change of the distance between the two is then,

\[z' = \frac{{\left( {300} \right)\left( {15} \right)}}{{460.9772}} = \require{bbox} \bbox[2pt,border:1px solid black]{{9.76187}}\]

b At what rate is the distance between the person and the rocket increasing 1 minute after liftoff? Show Solution

This part is nearly identical to the first part with the exception that the time is now 60 seconds (and note that we MUST be in seconds because the speeds are in time of seconds).

Here is the work for this problem.

\[\begin{align*}y = \left( {15} \right)\left( {60} \right) = 900\hspace{0.5in}z & = \sqrt {{{900}^2} + {{350}^2}} = \sqrt {932500} = 50\sqrt {373} = 965.6604\\ z' & = \frac{{\left( {900} \right)\left( {15} \right)}}{{965.6604}} = \require{bbox} \bbox[2pt,border:1px solid black]{{13.98007}}\end{align*}\]