Section 3.11 : Related Rates
9. A light is mounted on a wall 5 meters above the ground. A 2 meter tall person is initially 10 meters from the wall and is moving towards the wall at a rate of 0.5 m/sec. After 4 seconds of moving is the tip of the shadow moving (a) towards or away from the person and (b) towards or away from the wall?
Show All Solutions Hide All Solutions
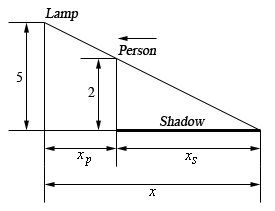
Start SolutionHere is a sketch for this situation that will work for both parts so we’ll put it here. Also note that we know that \({x'_p} = - 0.5\) for both parts.
a After 4 seconds of moving is the tip of the shadow towards or away from the person? Show All Steps Hide All Steps
Show Step 2
In this case we want to determine \({x'_s}\) when \({x_p} = 10 - 4\left( {0.5} \right) = 8\) (although it will turn out that we simply don’t need this piece of information for this problem….).
We can use the idea of similar triangles to get the following equation.
\[\frac{2}{5} = \frac{{{x_s}}}{x} = \frac{{{x_s}}}{{{x_p} + {x_s}}}\]If we solve this for \({x_s}\) we arrive at,
\[\begin{array}{lr}{\textstyle{2 \over 5}}\left( {{x_p} + {x_s}} \right) = {x_s} & \\ {\textstyle{2 \over 5}}{x_p} + {\textstyle{2 \over 5}}{x_s} = {x_s} & \hspace{0.5in} \Rightarrow \hspace{0.5in}{x_s} = {\textstyle{2 \over 3}}{x_p}\end{array}\]This equation will work perfectly for us.
Show Step 3Differentiation with respect to \(t\) will give us,
\[{x'_s} = {\textstyle{2 \over 3}}{x'_p}\] Show Step 4Finishing off this problem is very simple as all we need to do is plug in the known speed.
\[{x'_s} = {\textstyle{2 \over 3}}\left( { - 0.5} \right) = - {\textstyle{1 \over 3}}\]Because this rate is negative we can see that the tip of the shadow is moving towards the person at a rate of \({\textstyle{1 \over 3}}\) m/s.
b After 4 seconds of moving is the tip of the shadow towards or away from the wall? Show All Steps Hide All Steps
Show Step 2
In this case we want to determine \(x'\) and the equation is really simple. All we need is,
\[x = {x_p} + {x_s}\] Show Step 3Differentiation with respect to \(t\) will give us,
\[x' = {x'_p} + {x'_s}\] Show Step 4Finishing off this problem is very simple as all we need to do is plug in the known speeds and note that we will need to result from the first part here. So we have \({x'_p} = - {\textstyle{1 \over 2}}\) from the problem statement and \({x'_s} = - {\textstyle{1 \over 3}}\) from the previous part.
\[x' = - {\textstyle{1 \over 2}} + \left( { - {\textstyle{1 \over 3}}} \right) = - {\textstyle{5 \over 6}}\]Because this rate is negative we can see that the tip of the shadow is moving towards the wall at a rate of \({\textstyle{5 \over 6}}\) m/s.