Section 4.6 : The Shape of a Graph, Part II
2. Below is the graph the 2nd derivative of a function. From this graph determine the intervals in which the function is concave up and concave down.
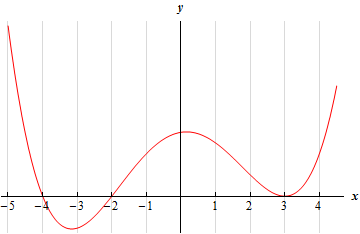
We need to be careful and not do this problem as we did the first practice problem. The graph given is the graph of the 2nd derivative and not the graph of the function. Therefore, the answer is not just where the graph is concave up or concave down.
What we need to do here is to recall that if the 2nd derivative is positive (i.e. the graph is above the \(x\)-axis) then the function in concave up and if the 2nd derivative is negative (i.e. the graph is below the \(x\)-axis) then the function is concave down.
So, it is fairly clear where the graph is above/below the \(x\)-axis and so we have the following intervals of concave up/concave down.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{{\mbox{Concave Up : }}\left( { - \infty , - 4} \right),\left( { - 2,3} \right)\,\,\,\& \,\,\,\left( {3,\infty } \right)\hspace{0.25in}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\mbox{Concave Down : }}\,\,\left( { - 4, - 2} \right)}}\]Even though the problem didn’t ask for it we can also identify that \(x = - 4\) and \(x = - 2\) are inflection points because at these points the concavity changes. Note that \(x = 3\) is not an inflection point. Clearly the 2nd derivative is zero here, but the concavity doesn’t change at this point and so it is not an inflection point. Keep in mind inflection points are only where the concavity changes and not simply where the 2nd derivative is zero.