Section 1.3 : Trig Functions
5. Determine the exact value of \(\displaystyle \tan \left( {\frac{{3\pi }}{4}} \right)\) without using a calculator.
Show All Steps Hide All Steps
First we can notice that \(\pi - \frac{\pi }{4} = \frac{{3\pi }}{4}\) and so (remembering that negative angles are rotated clockwise) we can see that the terminal line for \(\frac{{3\pi }}{4}\) will form an angle of \(\frac{\pi }{4}\) with the negative \(x\)-axis in the second quadrant and we’ll have the following unit circle for this problem.
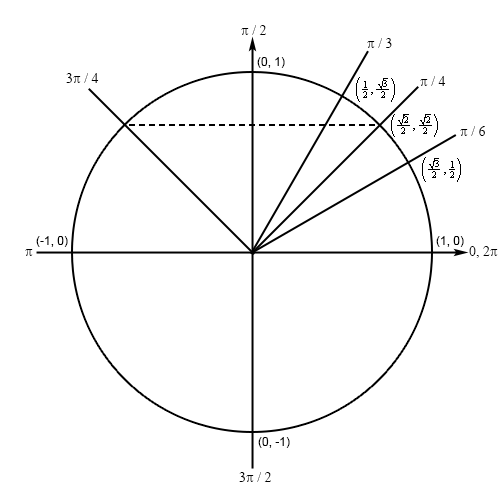
The coordinates of the line representing \(\frac{{3\pi }}{4}\) will be the same as the coordinates of the line representing \(\frac{\pi }{4}\) except that the \(x\) coordinate will now be negative. So, our new coordinates will then be \(\left( { - \frac{{\sqrt 2 }}{2},\frac{{\sqrt 2 }}{2}} \right)\) and so the answer is,
\[\tan \left( \frac{3\pi }{4} \right)=\frac{\sin \left( \frac{3\pi }{4} \right)}{\cos \left( \frac{3\pi }{4} \right)}=\frac{{}^{\sqrt{2}}/{}_{2}}{-{}^{\sqrt{2}}/{}_{2}}=-1\]