Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 1.3 : Trig Functions
6. Determine the exact value of \(\displaystyle \sec \left( { - \frac{{11\pi }}{6}} \right)\) without using a calculator.
Show All Steps Hide All Steps
Hint : Even though a unit circle only tells us information about sine and cosine it is still useful for secant so sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
First, we can notice that \(\frac{\pi }{6} - 2\pi = - \frac{{11\pi }}{6}\) and so (remembering that negative angles are rotated clockwise) we can see that the terminal line for \( - \frac{{11\pi }}{6}\) will form an angle of \(\frac{\pi }{6}\) with the positive \(x\)-axis in the first quadrant. In other words, \( - \frac{{11\pi }}{6}\) and \(\frac{\pi }{6}\) represent the same angle. So, we’ll have the following unit circle for this problem.
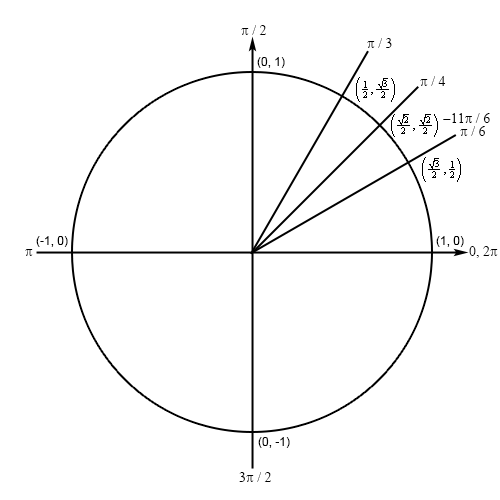
Hint : Given the obvious symmetry here use the definition of secant in terms of cosine to write down the solution.
Because the two angles \( - \frac{{11\pi }}{6}\) and \(\frac{\pi }{6}\) have the same coordinates the answer is,
\[\sec \left( -\frac{11\pi }{6} \right)=\frac{1}{\cos \left( -\frac{11\pi }{6} \right)}=\frac{1}{{}^{\sqrt{3}}/{}_{2}}=\frac{2}{\sqrt{3}}\]