Section 2.9 : Continuity
- The graph of \(f\left( x \right)\) is given below. Based on this graph determine where the function is discontinuous.
Solution
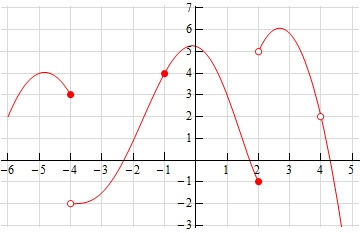
- The graph of \(f\left( x \right)\) is given below. Based on this graph determine where the function is discontinuous.
Solution
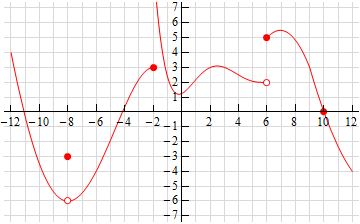
For problems 3 – 7 using only Properties 1 – 9 from the Limit Properties section, one-sided limit properties (if needed) and the definition of continuity determine if the given function is continuous or discontinuous at the indicated points.
- \(\displaystyle f\left( x \right) = \frac{{4x + 5}}{{9 - 3x}}\)
- \(x = - 1\)
- \(x = 0\)
- \(x = 3\)
- \(\displaystyle g\left( z \right) = \frac{6}{{{z^2} - 3z - 10}}\)
- \(z = - 2\)
- \(z = 0\)
- \(z = 5\)
- \(g\left( x \right) = \left\{ {\begin{array}{rl}{2x}&{x < 6}\\{x - 1}&{x \ge 6}\end{array}} \right.\)
- \(x = 4\)
- \(x = 6\)
- \(h\left( t \right) = \left\{ {\begin{array}{rl}{{t^2}}&{t < - 2}\\{t + 6}&{t \ge - 2}\end{array}} \right.\)
- \(t = - 2\)
- \(t = 10\)
- \(g\left( x \right) = \left\{ {\begin{array}{rc}{1 - 3x}&{x < - 6}\\7&{x = - 6}\\{{x^3}}&{ - 6 < x < 1}\\1&{x = 1}\\{2 - x}&{x > 1}\end{array}} \right.\)
- \(x = - 6\)
- \(x = 1\)
For problems 8 – 12 determine where the given function is discontinuous.
- \(\displaystyle f\left( x \right) = \frac{{{x^2} - 9}}{{3{x^2} + 2x - 8}}\) Solution
- \(\displaystyle R\left( t \right) = \frac{{8t}}{{{t^2} - 9t - 1}}\) Solution
- \(\displaystyle h\left( z \right) = \frac{1}{{2 - 4\cos \left( {3z} \right)}}\) Solution
- \(\displaystyle y\left( x \right) = \frac{x}{{7 - {{\bf{e}}^{2x + 3}}}}\) Solution
- \(g\left( x \right) = \tan \left( {2x} \right)\) Solution
For problems 13 – 15 use the Intermediate Value Theorem to show that the given equation has at least one solution in the indicated interval. Note that you are NOT asked to find the solution only show that at least one must exist in the indicated interval.