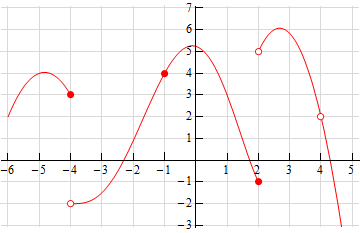
Before starting the solution recall that in order for a function to be continuous at $x = a$ both $f\left( a \right)$ and $\mathop {\lim }\limits_{x \to a} f\left( x \right)$ must exist and we must have,

$$\mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left( a \right)$$

Using this idea it should be fairly clear where the function is not continuous.

First notice that at $x = - 4$ we have,

$$\mathop {\lim }\limits_{x \to - {4^ - }} f\left( x \right) = 3 \ne - 2 = \mathop {\lim }\limits_{x \to - {4^ + }} f\left( x \right)$$

and therefore, we also know that $\mathop {\lim }\limits_{x \to - 4} f\left( x \right)$ doesn’t exist. We can therefore conclude that $f\left( x \right)$ is discontinuous at $x = - 4$ because the limit does not exist.

Likewise, at $x = 2$ we have,

$$\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = - 1 \ne 5 = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)$$

and therefore, we also know that $$\mathop {\lim }\limits_{x \to 2} f\left( x \right)$$ doesn’t exist. So again, because the limit does not exist, we can see that $f\left( x \right)$ is discontinuous at $x = 2$.

Finally let’s take a look at $x = 4$. Here we can see that,

$$\mathop {\lim }\limits_{x \to {4^ - }} f\left( x \right) = 2 = \mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right)$$

and therefore, we also know that $\mathop {\lim }\limits_{x \to 4} f\left( x \right) = 2$. However, we can also see that $f\left( 4 \right)$ doesn’t exist and so once again $f\left( x \right)$ is discontinuous at $x = 4$ because this time the function does not exist at $x = 4$.

All other points on this graph will have both the function and limit exist and we’ll have $\mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left( a \right)$ and so will be continuous.

In summary then the points of discontinuity for this graph are : $x = - 4$, $x = 2$ and $x = 4$.