Section 3.3 : Differentiation Formulas
17. The position of an object at any time t is given by \(s\left( t \right) = 3{t^4} - 40{t^3} + 126{t^2} - 9\).
- Determine the velocity of the object at any time t.
- Does the object ever stop moving?
- When is the object moving to the right and when is the object moving to the left?
Show All Solutions Hide All Solutions
Recall that one of the interpretations of the derivative is that it gives the velocity of an object if we know the position function of the object.
We’ve been given the position function of the object and so all we need to do is find its derivative and we’ll have the velocity of the object at any time \(t\).
The velocity of the object is then,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{s'\left( t \right) = 12{t^3} - 120{t^2} + 252t = 12t\left( {t - 3} \right)\left( {t - 7} \right)}}\]Note that the derivative was factored for later parts and doesn’t really need to be done in general.
The object will not be moving if the velocity is ever zero and so all we need to do is set the derivative equal to zero and solve.
\[s'\left( t \right) = 0\hspace{0.5in} \Rightarrow \hspace{0.5in}12t\left( {t - 3} \right)\left( {t - 7} \right) = 0\]From this it is pretty easy to see that the derivative will be zero, and hence the object will not be moving, at,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{t = 0 \hspace{0.25in} t = 3 \hspace{0.25in} t = 7}}\]To answer this part all we need to know is where the derivative is positive (and hence the object is moving to the right) or negative (and hence the object is moving to the left). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.
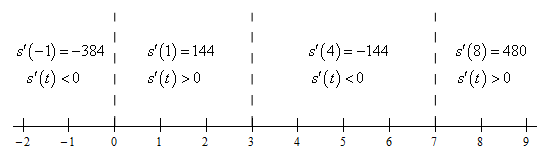
From this we get the following right/left movement information.
\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{align*}{\mbox{Moving Right :}} & \,\,\,\, 0 < t < 3, \hspace{0.25in} 7 < t < \infty \\ {\mbox{Moving Left :}} & - \infty < t < 0, \hspace{0.25in} 3 < t < 7\end{align*}}\]Note that depending upon your interpretation of \(t\) as time you may or may not have included the interval \( - \infty < t < 0\) in the “Moving Left” portion.