Section 3.3 : Differentiation Formulas
18. Determine where the function \(h\left( z \right) = 6 + 40{z^3} - 5{z^4} - 4{z^5}\) is increasing and decreasing.
Show All Steps Hide All Steps
Recall that one of the interpretations of the derivative is that it gives the rate of change of the function. Since we are talking about where the function is increasing and decreasing we are clearly talking about the rate of change of the function.
So, we’ll need the derivative.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{h'\left( z \right) = 120{z^2} - 20{z^3} - 20{z^4} = - 20{z^2}\left( {z + 3} \right)\left( {z - 2} \right)}}\]Note that the derivative was factored for later steps and doesn’t really need to be done in general.
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve.
\[h'\left( z \right) = 0\hspace{0.5in} \Rightarrow \hspace{0.5in} - 20{z^2}\left( {z + 3} \right)\left( {z - 2} \right) = 0\]From this it is pretty easy to see that the derivative will be zero, and hence the function will not be moving, at,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{z = 0 \hspace{0.25in} z = - 3 \hspace{0.25in} z = 2}}\]To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.
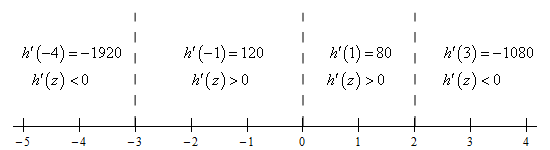
From this we get the following increasing/decreasing information.
\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{align*}{\mbox{Increasing :}} & \,\, - 3 < z < 0,\,\,\,\,\,0 < z < 2\\ {\mbox{Decreasing :}} & \,\, - \infty < z < - 3,\,\,\,\,2 < z < \infty \end{align*}}\]